为了便于描述，这里依然定义一个“世界”：
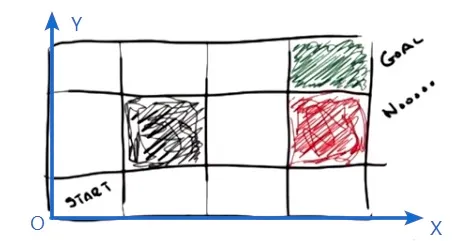
令空白格子的奖励为1.
Q-Table
Q-table 是 Q-learning 的核心。它是一个表格，记录了每个状态下采取不同动作，所获取的最大长期奖励期望。通过此，就可以知道每一步的最佳动作是什么。
Q-table 的每一列代表一个动作，每一行表示一个状态。则每个格子的值就是此状态下采取此动作获得的最大长期奖励期望。例如：
| U↑ | D↓ | L← | R→ | |
|---|---|---|---|---|
| START | ? | 0 | 0 | ? |
| (2,1) | 0 | 0 | ? | ? |
| (1,2) | ? | ? | 0 | 0 |
| … | … | … | … | … |
上表表示，对于状态 STRAT 向下或左的奖励期望是0（因为无法移动），其余两个方向由于未探索，所以奖励未知。状态(2,1)和状态(1,2)同理。
如果能求出整个表的所有值，那么这个问题就解决了。为了做到这一点，需要使用 Q-learning 算法。
Q-learning 算法
算法流程可以表述为：
- 初始化 Q-table.
- 选择一个动作 A.
- 执行动作 A.
- 获得奖励。
- 更新 Q. 并循环执行步骤2.
在这个流程中有两个地方需要注意。
如何选取动作
在一开始，表格中值都为0，自然地我们会想到随机选取一个动作。但随着迭代的进行，若一直随机选择，就相当于没有利用已经学习到的东西。为了解决这个问题，可能会想到除第一次外，均采取当前Q值最大的动作。但这样又可能陷入局部最优解，因为可能还有更好的动作没有被发现。
这其实是如何平衡「探索」与「利用」的问题。
于是可以采用一种叫做 ε-greedy 的策略。
ε-greedy 策略的本质就是：每次有ε概率进行探索，有(1-ε)的概率利用已学习的数据。探索意味着随机选取一个动作，利用意味着采取当前Q值最高的动作。
除了 ε-greedy ，还有一些效果更好的方法，但是复杂很多。
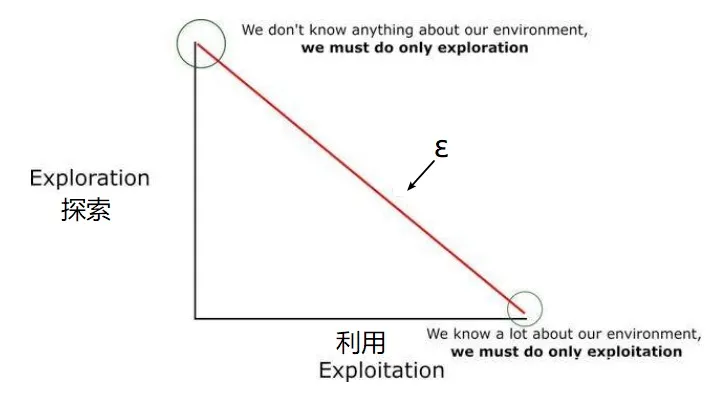
一开始往往设定一个较高的 ε（比如1），因为我们对环境一无所知，只能随机选择。随着迭代，可以逐步降低 ε，因为我们已经越来越准确地了解了环境。如下图所示：
如何更新 Q
$$ Q(s,a) \leftarrow (1-\alpha)Q(s,a)+\alpha \left [ R(s,a)+\gamma \max_{a'}Q(s',a')-Q(s,a) \right ] $$
这就是更新 Q 的函数，其中 α 为学习速率。显然，α 越大，保留之前学习的结果越少。