Markov 决策过程
Markov 决策过程中文译为马尔可夫决策过程。英文全称为 Markov Decison Processes，简称 MDP.
为了便于描述，首先定义一个“世界”，如下：
从起点开始，每次选择往四个方向走一格子。目标是到达绿色格子，游戏结束，碰到红色则失败，游戏结束。 黑色格子为障碍物，碰到障碍物或撞到墙壁则原地不动。 但是每次移动准确率只有80%，另外有20%的概率向与目标方向垂直的方向移动，这两个垂直的方向概率各是10%.
名词定义
- **STATES（状态）：**顾名思义，就是智能体当前的状态。在这个世界中，表现为「坐标」。则开始状态就是(1,1)，目标状态是(4,3).
- **ACTIONS（动作）：**即在一个特定的STATE中所做的事。在这个世界中表现为四向移动。
- **MODEL（转换模型）：**模型描述了整个游戏规则。可以抽象为有三个参数的函数：
T(s,a,s')，他生成的其实是一个概率：P(s'|s,a)，即：从状态s，采取动作a，转换到状态s'的概率。 - **REWARD（奖励）：**即到达一个状态得到的反馈。例如到达绿色格子可以获得正数奖励。所以可以表述为与状态有关的函数：
R(s)，也可以变形为R(s,a)或R(s,a,s'). - **POLICY（策略）：*上面三个定义组成了一个「问题」，则策略就是一个解决方案。它根据所处的状态，返回一个动作。可以表述为函数：
π(s) → a. 而 $ \pi^ $ 则表示最优策略，它最大化长期期望奖励。
从MODEL定义，可以得出 Markov 特性，即：下一个状态的产生只和当前状态有关。
不同奖励下的策略
无穷时域是前提假设，即：只要不进入红绿格子，游戏可以一直进行下去。
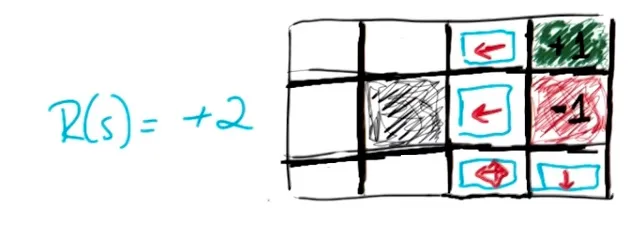
当空白格子奖励为+2，甚至大于目标格子的奖励。那么智能体就会尽可能地留着游戏中不出局。基于此，可得上图策略。
需要注意，第(3,3)格子不可以向下。若向下，则有10%概率结束游戏，若向左则不可能结束游戏。
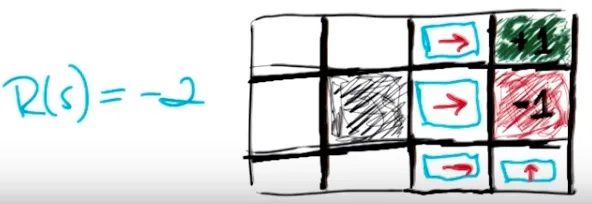
当空白格子奖励为-2，为了最大化长期期望奖励，智能体应该尽快结束游戏。基于此可得上图策略。
需要注意，第(3,1)格不可以向上。若向上则有10%概率向左，距离结束位置更远。
偏向稳定性
有一个关于状态序列的价值函数 V：
$$ V(s_0,s_1,s_2,...) = \sum_{t=0}^{\infty}R(s_t) $$
有这样一个事实：
若 $ V(s_0,s_1,s_2...) > V(s_0,s_1',s_2'...) $ 则有 $ V(s_1,s_2...) > V(s_1',s_2'...) $
同时，价值说明了延迟奖励的意义所在。即采取某一动作当时不会获得高额奖励甚至是负数奖励，但未来可以收获较多奖励。
折扣期望
引例
假设有下面两种奖励序列：
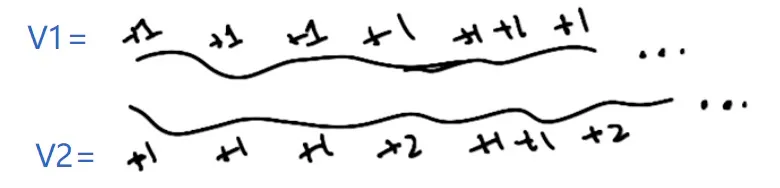
直观上可能会认为 V2 > V1，但是实际上 V2 = V1 = ∞. 实际与直观并不相符。即使这样，我们也可能更偏爱V2. 造成这种现象的直接原因就是时域是无穷的，进而导致奖励不断累积，长期期望奖励趋向于无穷大。
折扣
为了解决上述问题，可以改变一下函数 V.
$$ V(s_0,s_1,s_2,...) = \sum_{t=0}^{\infty}\gamma^t R(s_t) \leqslant \sum_{t=0}^{\infty}\gamma^t R_{max} ,0\leqslant \gamma < 1 $$
如此一来，随着时间推移，每一步获得的奖励会越来越小。不难看出这是一个等比数列求和：$ V = \frac{R_{max}}{1-\gamma} $
这就是折扣期望，也叫折扣数列或折扣总和。他实现了无穷到有穷的转变。即：可以一直走下去，但最终获得的总奖励是有限的。
最优策略
推导
根据定义，最优策略应该最大化长期期望奖励，即： $ \pi^* = \arg\max E\left [ \sum_{t}\gamma ^t R(s_t) \mid \pi \right ] $
那么在遵循π策略时的价值就应该是： $ V^\pi(s) = E\left [ \sum_{t}\gamma ^t R(s_t) \mid \pi ,s_0 = s \right ] $
需要注意，$ V(s)\neq R(s) $. 价值是一个长期的反馈，而奖励是进入某一状态的立即反馈。
在有了价值之后，可以优化一下最优策略的表达式： $ \pi^* (s) = \arg\max \sum_{s'}T(s,a,s')V(s') $
即：最大化 加总 进入状态s'的概率与它价值的积。 另外，如果遵循最优策略，那么这个价值就是最优策略价值。即 $ V(s)\equiv V^{\pi*}(s) $，称之为
状态的真实价值。 所谓最优策略就是：对于每一个状态，返回的动作能够最大化期望价值。
展开价值方程可得 Bellman 方程（贝尔曼方程）：
$ V(s) = R(s) + \gamma \max\sum_{s'}T(s,a,s')V(s') $
即：某个状态的真实价值 = 进入此状态得到的奖励 + 所有从此状态开始获得的奖励的折扣。
求解 Bellman 方程
由于实际上有n个状态，所以实际上这是一个n元方程组，包含n个方程。（R/T已知，V未知）
值迭代
思路：
- 从任意价值开始。
- 基于他们临近的状态更新这个价值。
- 重复第二步。
假设每次更新时间为t，则第二步方程可表述为： $$ \hat{V}(s){t+1} = R(S) + \gamma \max_a\sum{s'}T(s,a,s') \hat{V}_t(s') $$
此算法叫做值迭代。
实例：
$ \gamma=1, R(s)=-0.04, V_0(s)=0 $ 对于状态x，求两次迭代后的价值值 $ V_1(x), V_2(x) $
第一次迭代： 初始价值都是0，对于状态x显然往右走期望最大。因此： $ V_1(x)=-0.04+0.5\times (0.1\times0+0.1\times0+0.8\times1)=0.36 $ 同理，对于状态(3,2)，显然向左走期望最大，为0. 其他方向均小于0. 因此： $ V_1(3,2)=-0.04+0.5\times (0.1\times0+0.1\times0+0.8\times0)=-0.04 $
第二次迭代： 对于状态x，依然是向右期望最大。因此： $ V_2(x)=-0.04+0.5\times (0.1\times0.36+0.1\times-0.04+0.8\times1)=0.376 $
策略迭代
思路：
- 从任意的一个 $ \pi_0 $ 开始。
- 对于给定的 $\pi_t$，令 $V_t=V^\pi_t$.
- 更新 $ \pi_{t+1}=\arg\max_a\sum T(s,a,s')V_t(s') $.