博弈论（一）

在之前的讨论中，一场游戏只有一个智能体。而在博弈论中，智能体评估它们的决策如何与其他人的决策相互作用以产生不同的结果。

简单博弈

看一个具体的博弈游戏：

圆圈中的数字代表一个状态。L/R/M 代表智能体可采取的动作。叶子节点的数字代表智能体 A 的得分（B的得分是相反数)

首先 A 做出一个选择（动作），随后 B 做出一个动作，然后 A 可视情况再次做出一个动作。

博弈论一个基本前提是：假设所有玩家都想最大化自己的得分，并都可以正确做出最佳动作，并都相信其他玩家也会这样做。

这是博弈问题最简单的一种：两个玩家的零和有限确定性完美信息博弈。

• **两个玩家：**顾名思义，就是在这个博弈游戏中只有2个玩家（智能体）。
• **零和：**两个玩家获得的奖励（得分）之和是一个常量。（不一定为0）
• **有限性：**显然，这场博弈的一切元素例如：状态、动作等都是有限的。
• **确定性：**从 MDP 角度理解，即博弈中没有随机转换。从某一状态采取某一动作得到的结果是确定的。
• **完美信息：**我们能够确定当前智能体所处的状态。 <!-- more -->

STRATEGIES（策略）

在 MDP 中有个名词叫 POLICIES （策略），它是状态到动作的映射。博弈论中有类似的概念，称为 STRATEGIES （策略），它是所有可能的状态到动作的映射。

对于 A 来说 (1→L, 4→L) 就是一个策略。不难看出，在这个特定的游戏中，A 有4个策略，B 有3个策略，如下：（这种策略被称为纯策略）

A:
(1→L, 4→L)  (1→L, 4→R)
(1→R, 4→L)  (1→R, 4→R)

B:
(2→L, 3→R)  (2→M, 3→R)  (2→R, 3→R)

我们可以以表格的形式写出这些策略，并在中间填入最后的得分。（由于B得分是A的相反数，所以这里省略B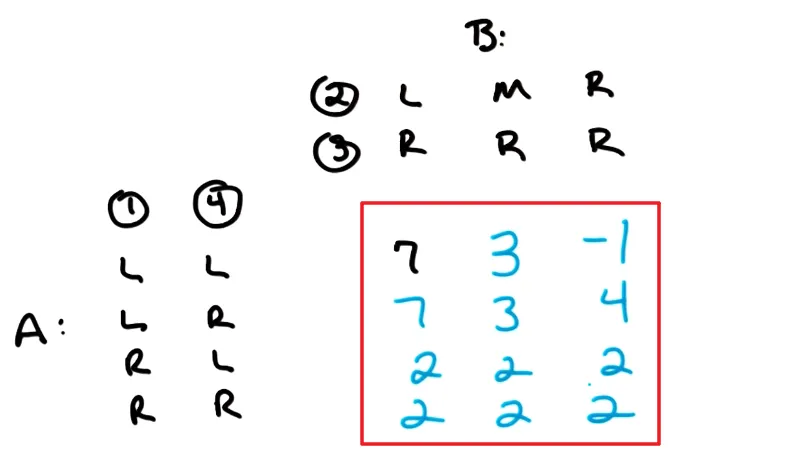） 最终可以得到一个矩阵（红框部分），这个矩阵包含了此场博弈的一切信息，即：有了它我们不再需要一开始的博弈树了。

极小极大原理

试想这样一个游戏过程：

A 为了最大化得分，也许会选择策略 (L,L) 或策略 (L,R) ，也就是矩阵的前两行。因为只有这样才有可能得到最高分7. 然而 B 同样希望最大化自己的得分，所以在 A 先选择的情况下，B 自然会选择当前状态下对自己最有利的。例如当 A 选择 (L,L)，B 就会选择 (R,R). 最后 A 得分 -1. 于是 A 没有达到一开始的目标。

A 总是最大化得到的分数，而 B 总是试图最小化 A 可以得到的分数。所以得出这样一个结论：A 先手时必须要考虑会遭遇 B 最严酷的反制策略。所以选择 (L,L) 是非常不明智的。事实上若交换 AB 角色，结论是一样的。

在这个结论的指导下，A 要选择的并不是全局最大值，而是在 B 执行反制策略（找到极小值）后得到尽可能大的值。也就是：极大化极小值。相反，B 要找到极小化极大值。（因为值越小 B 得分越高）

所以正确的博弈过程是这样的：

A 选择 (L,R), B 选择 (M,R)，最后 A 得分3. 即使是 B 先手，B 也应该选择 (M,R)，随后 A 选择 (L,R)，最终 B 得分-3. 虽然 B 依然失败，但它已经尽可能拿到了最高的分数。

从这个过程可以得出一个结论：极大化极小值和极小化极大值最终的结果是一样的。

极小极大原理也就是 Von neumann 定理（冯诺依曼定理）。

不确定性的博弈

前面所述简单博弈具有确定性，现在我们取消这一约束。看一个具体的游戏：

和之前很类似，但 A 在第一个状态采取动作 L 之后，有0.5的概率获得4分，也有0.5的概率获得-20分。这就是不确定性。

同样的，只需要用概率乘以得分再求和，也可以写出一个博弈矩阵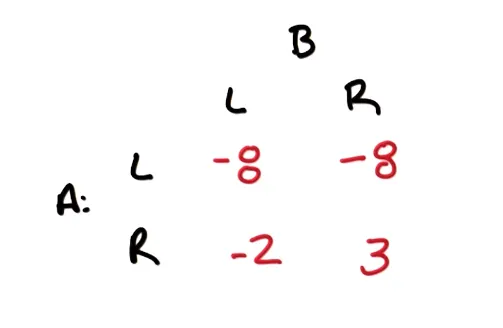： 不难看出，Von neumann 定理在不确定博弈中依然有效。于是可以将它的适用范围推广到：两个玩家的零和有限完美信息博弈。

隐藏信息博弈

前面所述博弈是完美信息，现在我们取消这一约束成为两个玩家的零和有限隐藏信息博弈。

看一个具体的游戏：

A 摸一张卡片，可能是红色或黑色，概率各是50%. （对于 A 来说红色是惩罚黑色是奖励） A 可以选择弃牌或保留。若弃牌则失去20元。 若 A 保留，B 可以弃权或要求亮牌。若 B 放弃则 A 获得10元。 若 B 要求亮牌，若是红色则 Ａ 失去40元；若是黑色 A 获得30元。 对于一个博彩游戏，A 失去也就是意味着 B 获得，所以是零和的。

因为 B 不知道 A 抽到的是什么颜色，故不知道自己处在哪一状态，也就是隐藏信息。

同样的可以得到一个矩阵：

不难看出，在这场博弈中，Von neumann 定理不再有效了，它无法在不同情况下得出一个确定的结果。

混合策略

混合策略与纯策略的区别就是，需要指定选择不同策略的概率。如此看，纯策略是特殊的混合策略，其选择某一策略的概率是100%.

令 A 选择留牌的概率是 p，那么当 B 选择弃权时，A 的预计收益是 $ 10p-5(1-p)=15p-5 $. 当 B 选择亮牌时，A 的预计收益是 $ -5p+5(1-p)=-10p+5 $.

不难看出这是2个关于p的函数，可以把它画出来：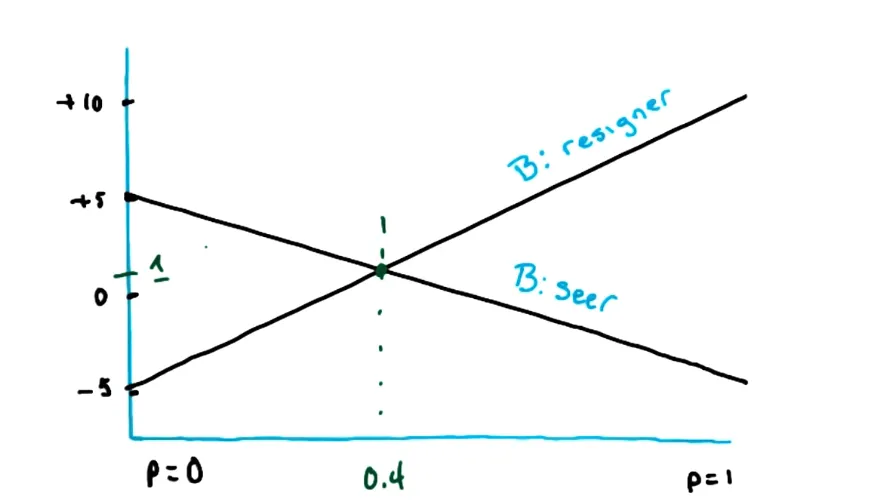

由于 B 始终希望最小化 A 的奖励，所以 A 实际的奖励函数应该是取最小的部分（下图红色部分），也就是极大化极小值。 同样的，黄色部分是极小化极大值。他们最终应该选取的点相同。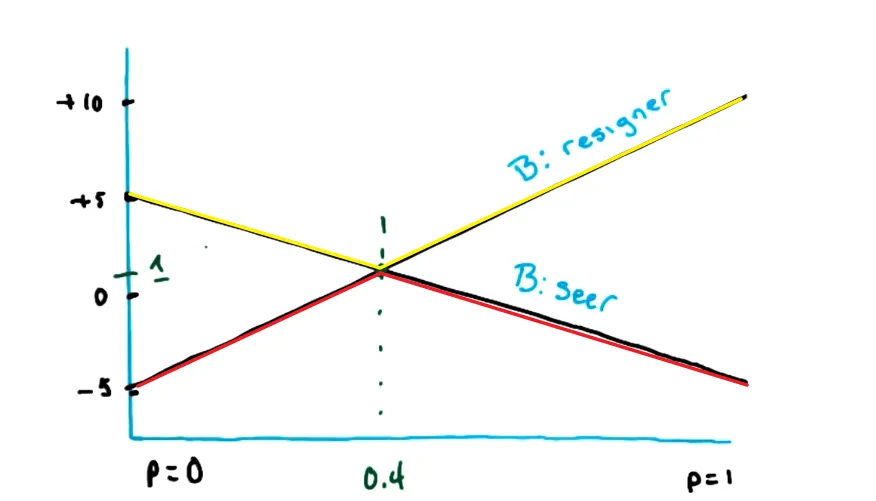

非零和

前面所述博弈是零和的，现在我们再取消这一约束成为两个玩家的非零和有限隐藏信息博弈。

同样，先看一个具体的博弈：

两个嫌疑人因抢劫被抓获，被隔离审讯。若其中一人背叛同伙而向警方检举另一个人，他将获得释放，被检举的人将获刑9个月。 若双方同时检举对方，则均判刑6个月。 若双方互相合作都不主动揭发，则均因证据不足被轻判为1个月。

类似地，可以表述为一个矩阵。但由于这里不是零和了，因此 AB 双方的得分都需要列出。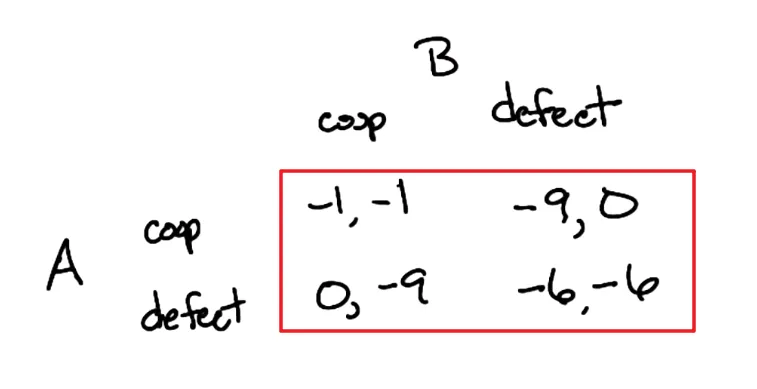

囚徒困境

显然，相互合作不揭发对于这个犯罪团伙是最好的方案。但实际上并非那么顺利。设想下面的情况：

对于 A 来讲，假设 B 选择合作，那么为了最大化自己利益 A 会选择检举；假设 B 选择检举，同样为了最大化自己利益，A 还是会检举。 对于 B 来讲情况是一样的，无论 A 如何选择 B 都会选择检举。

因此最终他们会互相检举从而均被判刑6个月，这不是想要的最佳方案。这被称为 囚徒困境。

NASH 均衡

NASH 均衡，英文 nash equilibrium ，也被音译为纳什均衡。

当且仅当对于所有的 n 个玩家，各自选择的每一项策略都使此玩家效用最大，即为 Nash 均衡。 更好理解的解释是：当所有玩家都知道其他玩家的策略，任意选择一名玩家允许他改变策略，他都没有理由改变，因为当前策略可以最大化效用。

Nash 均衡的定义适用于纯策略和混合策略。

严格控制

对于这个具体博弈，A 选择检举（第二行）总是要比合作（第一行）更有利（0>-1, -6>-9）。可以称为第二行严格控制第一行。

这也就意味着如果选择了第一行的任何数据，那么总是应该倾向于选择下一行，因为它更有利。

NASH 均衡的基本定理

• 在 n 个玩家的纯策略博弈中，如果淘汰所有经过严格控制的策略，只留下一组策略，那么这一组策略就是唯一的 Nash 均衡。
• 任何的 Nash 均衡都将在反复删减的严格劣势策略过程中留存下来。
• 如果玩家数量(n)是有限的，对于每一组策略，该组策略也是有限的。

连续囚徒困境博弈

在囚徒困境中，整个团体无法达成最佳策略。那么对于一个连续的囚徒困境博弈问题，是否可以通过先驱的博弈建立信任从而达到最佳呢？可惜答案也是否定的。

假设连续进行20场博弈，对于最后一场博弈来说，可以认为由于建立了信任，对方一定选择合作，基于最大化自己利益，这正是检举对方的好时机。因为双方都有这种想法，于是再次落入了囚徒困境。 因为第20次博弈结局已知，所以第19次博弈可看做是最后一次，根据归纳法不难看出，每一次博弈都将陷入囚徒困境。