LeetCode450 - 删除二叉搜索树中的节点

题目

传送门

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

分析

这是一道 Medium 难度的题目，主要是被删除的节点要分多种情况处理。一共有三类四种情况。

1. 被删除的节点是叶子。
2. 被删除的节点只有一个孩子。
3. 被删除的节点有两个孩子。

删除的节点是叶子

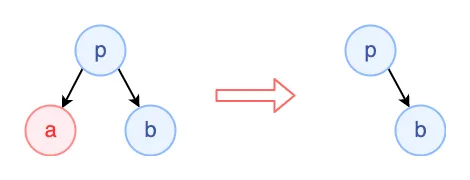
这是最简单的一种情况，只要删除这个节点就行了。

删除的节点只有一个孩子

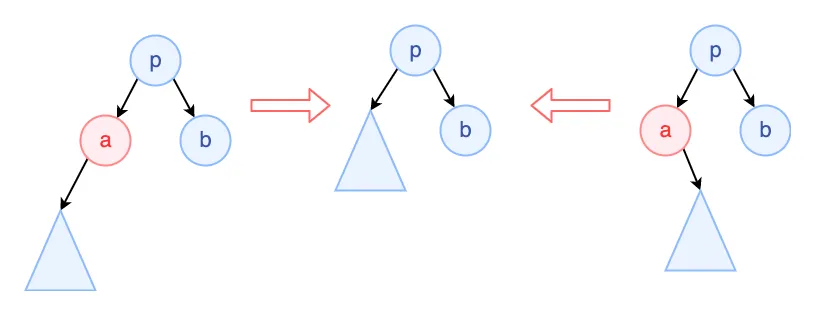
这种情况也不难，直接把那唯一的孩子（子树）接上去就行了。不管是左孩子还是右孩子，根据 BST 的性质，都是小于 p 的，因此接上去后依然是 BST。

删除的节点有两个孩子

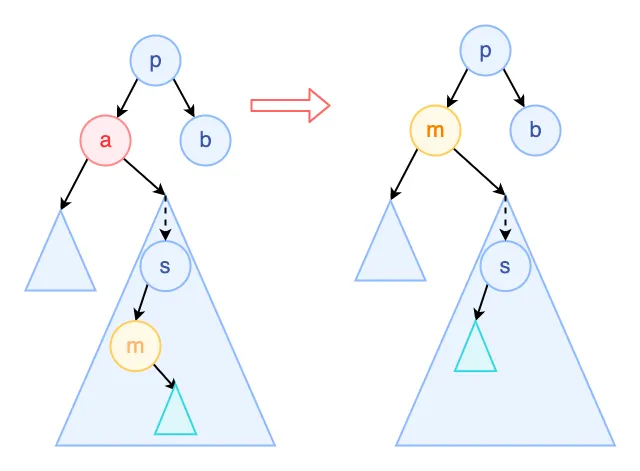
这种情况就比较复杂了。首先要从右子树里找到最小的一个元素 m，用它补上原来 a 的位置。然后 m 原先的右子树直接作为 m 原先父节点 s 的左子树。这种做法之所以行得通，是因为：

1. a 的左子树 < a < m < a 的右子树 < p。因此替换后 m 的左子树均小于 m，右子树均大于 m 且 m自身小于 p。
2. m 原来的右子树均小于 s，所以可以作为 s 的左子树。

实现

前两个类别基本上没有异议，第三个则有两种方案。

修改元素值

我们不真正删除节点 a，而是把 a 的值改成 m，然后在右子树中查找并删除 m。此时便退化到前两种简单的类别。

这种实现代码稍微简单。但是树的操作中，一般我们默认节点是不可变的，所以还是建议不要偷这个懒。

修改指针

这种实现则实实在在把 a 替换成 s，没什么好说的。

java 代码

这里提供修改指针的实现方案。注意体会下利用递归，我们无需手动保存要删除节点的父节点了。

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) return null;
        if (key < root.val)
            root.left = deleteNode(root.left, key);
        else if (key > root.val)
            root.right = deleteNode(root.right, key);
        else {
            // root 就是要删除的节点
            if (root.left == null)
                return root.right; // 是叶子或只有右子树
            else if (root.right == null)
                return root.left; // 是叶子或只有左子树
            TreeNode s = root; // min 的父节点
            TreeNode min = root.right; // 右子树中最小的节点
            while (min.left != null) {
                s = min;
                min = min.left;
            }
            if (s != root) {
                s.left = min.right;
                min.right = root.right;
            }
            min.left = root.left;
            return min;
        }
        return root;
    }
}