LeetCode279/127/126 - 用图建模
题目
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
坑 - 贪心算法
既然所求的是最少数量,很容易想到贪心算法:每次都找一个能取到的最大完全平方数,以此类推。
其实示例1恰恰就是一个反例。对于 n=12,最大的是 3<sup>2</sup>=9,然后只能连续取三个1,最后需要 4 个数,答案错误。
这也是贪心算法的典型缺陷——容易陷入局部最优解。
图论
这道题可以建模为图。
数字 [0, n] 每一个数是一个点。如果两点之差是一个完全平方数,则从大到小连接一条边,最终成为一个有向无权图。原问题转化为:求从节点 n 到 0 的最短路径长度。
简单起见,令 n=6,那么图如下所示:
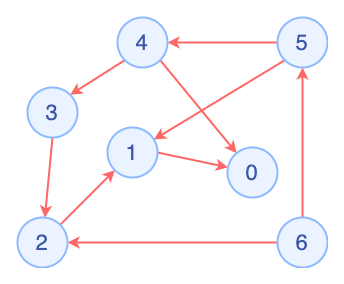
不要真正建图
尽管我们按照图的模型来建模,但不意味着要先建出完整的图再来执行广度优先遍历,那样就本末倒置了。
BFS 核心的一步是,每遍历到一个节点,就把与之相连的节点全部加入到队列中。所谓「与之相连的节点」在本题的环境下,就是「与当前节点数值之差是完全平方数」,那么通过一个循环就能轻松解决了:
for (int i = 1; num - i * i >= 0; i++) {
q.add(num - i * i);
}
然后就是注意几个优化的地方:
- 设立
visited数组,避免重复入栈。 - 在入栈时就判断是否为 0,不要等出栈再算。
num - i* i避免多次计算。
java 代码
class Solution {
public int numSquares(int n) {
Queue<Integer> q = new LinkedList<>();
q.add(n);
int step = 0;
boolean[] visited = new boolean[n + 1];
visited[n] = true;
while (!q.isEmpty()) {
int len = q.size();
for (int j = 0; j < len; j++) {
int num = q.poll();
for (int i = 1; ; i++) {
int a = num - i * i;
if (a < 0)
break;
if (a == 0)
return step + 1;
if (!visited[a]) {
q.add(a);
visited[a] = true;
}
}
}
step++;
}
throw new IllegalArgumentException();
}
}
扩展
127. Word Ladder
利用相同的思想也可解决 LeetCode 127. Word Ladder 问题。在这个情境中,「与之相连的节点」相当于「与当前单词只差 1 个字母的单词」,这就要遍历题目给出的列表,写一个函数来判断是否满足条件:
private boolean canTransform(String from, String to) {
if (from.length() != to.length())
return false;
int n = 0;
for (int i = 0; i < from.length(); i++)
if (from.charAt(i) != to.charAt(i)) {
n++;
if (n > 1) return false;
}
return n == 1;
}
126. Word Ladder II
在 127 的基础上衍生出这道题(传送门),算是比较难的一个了。与前面不同的是,既要求出所有最短的路径,还要把它们保存下来。不难看出有两个关键点:
- 求所有最短路径:BFS 找到一个结果后不能直接 return 了,而是要把这一层遍历完。
- 保存下来:队列里不能仅存节点信息,而是要保存整个路径(List),列表的最后一位是下次要访问的节点。
修改后的代码如下:
public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
List<List<String>> res = new LinkedList<>();
Set<String> visited = new HashSet<>();
Queue<LinkedList<String>> q = new LinkedList<>();
q.add(new LinkedList<>(List.of(beginWord)));
while (!q.isEmpty()) {
boolean find = false; // 当前层是否找到了结果
int len = q.size();
for (int i = 0; i < len; i++) {
LinkedList<String> path = q.poll();
visited.add(path.getLast());
for (String to : wordList) {
if (!visited.contains(to) && canTransform(path.getLast(), to)) {
if (to.equals(endWord)) { // 找到了最近的 END 节点
find = true;
path.add(to);
res.add(path);
break;
}
LinkedList<String> newPath = new LinkedList<>(path);
newPath.add(to);
q.add(newPath);
}
}
}
if (find) break;
}
return res;
}
与一开始的 279 号题目不同,这题需要进行更多节点的扫描,同时寻找下一个节点的操作也比较复杂,所以「一边建图一边遍历」不再合适了。现在我们希望一次性建好图,后面算法直接在图的基础上进行。优化后代码如下:
Map<String, List<String>> graph;
public List<List<String>> findLadders(String beginWord, String endWord, List<String> wordList) {
initGraph(wordList, beginWord);
List<List<String>> res = new LinkedList<>();
Set<String> visited = new HashSet<>();
Queue<LinkedList<String>> q = new LinkedList<>();
q.add(new LinkedList<>(List.of(beginWord)));
while (!q.isEmpty()) {
boolean find = false; // 当前层是否找到了结果
int len = q.size();
for (int i = 0; i < len; i++) {
LinkedList<String> path = q.poll();
visited.add(path.getLast());
if (!graph.containsKey(path.getLast()))
continue;
for (String to : graph.get(path.getLast())) {
if (visited.contains(to)) continue;
if (to.equals(endWord)) { // 找到最近的 END 节点
find = true;
path.add(to);
res.add(path);
break;
}
LinkedList<String> newPath = new LinkedList<>(path);
newPath.add(to);
q.add(newPath);
}
}
if (find) break;
}
return res;
}
private void initGraph(List<String> words, String begin) {
graph = new HashMap<>();
graph.put(begin, words.stream().filter(to -> canTransform(begin, to)).collect(Collectors.toList()));
words.forEach(wd -> {
graph.put(wd, words.stream().filter(to -> canTransform(wd, to)).collect(Collectors.toList()));
});
}