LeetCode149 - 直线上最多的点数

题目

传送门

给定一组 X-Y 平面上的点，返回位于同一条直线上的最大点数。

例子：

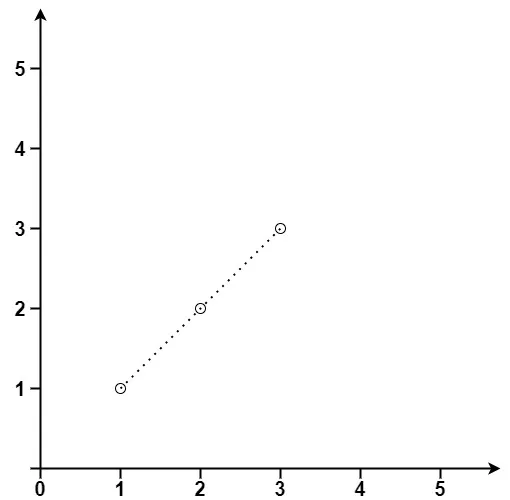
Input: points = [[1,1],[2,2],[3,3]]
Output: 3

约束：

• 1 <= points.length <= 300
• points[i].length == 2
• -104 <= xi, yi <= 104
• 没有重复的点

分析

这是一个 hard 级别的题目，但私以为主要是细节要考虑全面，整体思想倒不是很难。

题目已经限制了最多有 300 个点，那么 n² 的时间复杂度是可以接受的。以此为出发点，众所周知两点可以确定一条直线，那么只要计算出任意两点的直线，就可以判断其他的点在不在这条线上了。这里选择使用「点斜式」来表示直线，以便通过哈希表迅速完成「点是否在线上」的判断。

那么出现了两个细节问题：

1. 斜率有可能不存在。
2. 斜率会有误差。

问题 1 比较简单，单独判断一下就好。问题 2 则采用一个通用的办法来规避：String 代替 Double。具体来讲，要找出两个数的最大公约数，分别除以它化成最简分式的形式。例如 20/6=3.3333333 现在直接把字符串 10/3 当作 key 就好了。

java 代码

class Solution {
    public int maxPoints(int[][] points) {
        if (points.length <= 2)
            return points.length;
        int result = 0;
        for (int i = 0; i < points.length; i++) {
            Map<String, Integer> map = new HashMap<>(); // 斜率 -> 点个数
            for (int j = 0; j < points.length; j++) {
                if (i == j) continue;
                String slope = calcSlope(points[i], points[j]);
                map.put(slope, map.containsKey(slope) ? map.get(slope) + 1 : 2);
            }
            for (int c : map.values())
                if (c > result) result = c;
        }
        return result;
    }

    private String calcSlope(int[] p1, int[] p2) {
        if (p1[0] == p2[0]) // 斜率不存在
            return "N";
        int dx = p1[1] - p2[1];
        int dy = p1[0] - p2[0];
        int g = gcd(dx, dy);
        if (g != 0) {
            dx /= g;
            dy /= g;
        }
        return dx + "/" + dy;
    }

    private int gcd(int x, int y) {
        if (y == 0) return x;
        return gcd(y, x % y);
    }
}