支持中文的多模式匹配—AC自动机
本文使用 java (kotlin) 实现一个支持中文模式串的 AC 自动机算法。
简介
今天项目上出现了多个字符串匹配的需求,我这个算法弱鸡也被迫营业解决这个头疼的问题。
说到字符串匹配,首当其冲的就是大名鼎鼎 KMP,光是大学时期,就不知道成为多少学子的噩梦了。私以为,KMP 难以理解的关键在于搞不清楚为什么可以按照失败数组那样移动,而不用担心漏掉子串。但这不影响我们感受它的核心思想——充分利用曾经匹配的结果,避免无用功。
可惜 KMP 只能解决两个字符串之间的搜索。那如果是 1:N 呢?我们可以进行 N 遍 KMP。(不是) 又不是不能用✌️。但显然这不是一个好的办法。我们想,如果只扫描文本串一遍,就可以找出所有匹配该多好。
那么就是 AC 自动机辣,与 KMP 齐名的多模式匹配算法。几乎所有的敏感词识别,都是在此基础上实现的。它可以做到时间复杂度与关键字规模无关,只与主串有关。
AC 算法主要需要两部分数据,一是字典树,二是失败指针。前者用于查找,后者用于优化失配时的性能。
字典树
字典树也叫 trie 树,这里用来存储所有模式串,可以高效地进行查找。如下图,就是一个由模式串集合 { he, hers, his, she, shy } 构成的字典树,其中红色节点表示一个模式串的结束。

链接存储
在实际程序中,字典树可以有许多存储方式,最通俗易懂的自然是链接存储。我们可以建立一个 AcNode 类作为节点,通过内部字段的方式将各个节点连接起来,例如:
private static class AcNode {
Map<Character, AcNode> children;
int len = 0; // 0 表示这不是一个模式串的结束,否则表示模式串长度
}
注意,这里使用 Map 来记录孩子节点,以便我们可以快速查找是否存在相应的字符。使用 Character 作为数据类型可以获得原生的中文支持。
看起来非常完美,但其实使用 char 为 key 的 map 存在潜在的性能问题。每一次取值时不得不进行一次 unicode 解码,进而带来额外的开销。
数组存储
数组存储是另一个极端,借助随机存取的特性我们可以获得极高的性能,但同时也浪费了很多内存。

构造一个 MxN 的矩阵。其中 M 为模式串总计字符个数,N 为模式串中可能出现的字符种类个数(示例图中为 a-z)。则每一行代表一个节点,若节点中包含某个字符,则对应位置的元素设置为孩子节点的下标。-1 表示没有此字符。实际上 M 是个数上限,为了节约空间,可以使用动态数组。
这样说太抽象了,上图对应的数组表示法如下所示,我们结合这个数组来解释一下:
int[][] A = [
0-> [-1 ... 1(h) ... 2(s) ... -1],
1-> [-1 ... 3(e) ... 4(i) ... -1],
2-> [-1 ... 5(h) ... -1],
3-> [-1 ... 6(r) ... -1],
4-> [-1 ... 7(s) ... -1],
....
]
A[0] 代表根节点,A[0][0]=-1 代表根节点不包含字符 a。A[0][7]=1 代表根节点包含字符 h,并且对应的孩子节点是 A[1]。那么 A[1][4]=3 就代表 A[1] 这个节点包含字符 e,其对应的孩子节点是 A[3]。以此类推。
相比于 Map,这种结构可以在一瞬间找到是否包含某字符。既无需进行 unicode 解码,也无需进行哈希运算,更不存在哈希冲突的可能性。缺点也是显而易见,浪费了大量的空间来存储本来就不存在的字符。对于中文这种有很多单字的语言,此方案完全不可行 ❌
Byte 数组存储
来总结一下数组存储不可行的根本原因:
- 利用了英文字母与 int 的天然对应关系来规避 HashMap,但是中文没有此关系。
- 每一个基本字符对应一个元素。英文只有26个,而中文有上万个。
那么逐个击破。
我们知道任何数据都是二进制表示的,那么中文必然可以拆成一串 01,也就是 byte[]。而 byte 天然和 int 有对应关系。
另外,拆成 01 后,基本字符就只有 2 个。但这太过分了,只用 01 表示的话,这个树会巨高,影响查找性能。退而求其次,byte 基本字符(状态)只有 256 个,相对来说可以接受。
那么新方案呼之欲出,我们把字符串看作 byte 数组,每一个 byte 视为一个“字符”,直接对 byte 进行建模与查找。
到这里有的同学会问:
你这不还是进行 unicode 解码了吗?
答:是的,但是只解了一次,那就是构造字典树的时候。而一开始的 Map 方案,每遍历一个字符都要解码一次,多次查找还要多次解码。
最后,还有一个小小的副作用需要解决。标准的 AC 算法中,我们在每个模式串的结束节点记录了长度,匹配到此的时候,就可以使用 substring() 之类的函数直接得到模式串。现在呢?简单!改成记录 byte 长度,然后取字节数组子集,再编码回字符串👌<-- 这个答案是正确的。但为何不直接记录模式串本身呢?省的来回编码解码。
private final ArrayList<AcNode> nodes = new ArrayList<>();
private static class AcNode {
/** 模式串。null 表示此节点不是模式串的结尾。 */
String pattern = null;
/** 子节点在 #nodes 的下标。-1 表示相应 Byte 没有子节点。children 下标即代表 Byte 数据。 */
int[] children = new int[BYTE_SIZE];
AcNode() {
Arrays.fill(children, -1);
}
}
究竟是否需要牺牲空间换时间,就看实际需求啦。
构造代码
确定了数据结构,构造字典树相对来说非常简单。
private static final int BYTE_SIZE = Byte.MAX_VALUE - Byte.MIN_VALUE + 1;
private final AcNode root = new AcNode();
private final ArrayList<AcNode> nodes = new ArrayList<>();
void insert(@NotNull String key) {
AcNode p = root;
byte[] bytes = key.getBytes(StandardCharsets.UTF_8);
for (byte b : bytes) {
int i = b - Byte.MIN_VALUE;
if (p.children[i] == -1) {
// 不包含所需节点,创建
AcNode newNode = new AcNode();
nodes.add(newNode);
p.children[i] = nodes.size() - 1;
}
p = nodes.get(p.children[i]);
}
p.pattern = key;
}
如上,每次插入一个模式串,我们将其转为 byte 数组,以 byte 为单位进行构造。通过 byte - Byte.MIN_VALUE 实现了 byte 本身与数组下标的自然对应,不再需要哈希函数。
失败指针
介绍
和 KMP 一样,AC 的失败指针也是指示了匹配失败时要跳转到的位置,核心目的同样是充分利用之前匹配的结果,避免每次都从头开始。依然是类比 KMP,AC 失败指针的实质是寻找最长后缀,使之能够被匹配。例如模式集合 {she, hers},匹配字符串“shers”时,在 e 的位置失配(she 这条路径接下来没有 r),那么它的最长后缀 he 是能够从根节点匹配的,所以我们沿着 he 这条路径,从 e 接着向下,最终成功匹配 hers。
失败指针构造算法如下:
-
根节点失败指针为 null。
-
对于节点
curr,其父亲节点的失败指针指向temp。- 若
temp不存在,那么curr的失败节点就是根节点。(即失败指针指向 root) - 若
temp存在,并且temp节点存在当前要匹配的字符,那么curr的失败节点就是temp中要匹配字符的那个孩子节点。 - 若
temp存在,但也无法匹配当前字符,那么将temp的失败节点作为新的temp循环查找。
- 若
⚠️ 注意,这里与标准 AC 有些不同。理论上,如果失败节点本身是一个模式串的结尾,那么要把这个模式串加入到当前节点。这个操作便于实现这样一种效果:对于集合 {ab, bc},字符串 "abc" 同时匹配 ab 与 bc。但是我的需求略有不同,要求一个字符只能被消费一次,也就是说 b 被 ab 消费了,那么就不能再组成 ac。因此这里不进行这个额外操作。

因为失败指针的构造需要用到父节点的失败指针,所以按照层序最为合适。
-
对于节点
2,其父节点为 root,失败指针不存在,故 2 的失败节点为 root。节点3同理。 -
对于节点
4,其父节点为2,2 的失败节点为 root,但是 root 不存在字符e,故继续查找 root 的失败指针,不存在,故4的失败节点为 root。节点5同理。 -
对于节点
6,其父节点为3,3 的失败节点为 root,并且 root 存在字符h, h 对应节点2,故6的失败节点为2。其他节点同理。这里要强调的是节点
9,其父节点为6,6 的失败节点为2,并且 2 存在字符e,e 对应节点4,所以9的失败节点为4。除此之外,4本身也是模式串he的结尾,理论上要把4的模式串信息添加到9,即9的模式串长度有两个,L = {3, 2},这里由于前述需求的不同,不执行此操作。
构造代码
private final ArrayDeque<Integer> q = new ArrayDeque<>(); // 用于层序遍历的队列
private int[] fail;
void calcFail() {
q.clear();
fail = new int[nodes.size()];
Arrays.fill(fail, -1);
q.addLast(0);
while (!q.isEmpty()) {
int fatherIndex = q.pop();
AcNode father = nodes.get(fatherIndex);
for (int i = 0; i < father.children.length; i++) {
if (father.children[i] == -1) {
continue;
}
int currIndex = father.children[i];
int temp = fail[fatherIndex]; // temp 为当前节点 curr 父节点的失败指针
while (temp != -1 && nodes.get(temp).children[i] == -1) {
// 若父亲的失败节点不为空,但是不存在公共后缀,则继续向上从这个节点的失败节点寻找
temp = fail[temp];
}
if (temp == -1) {
fail[currIndex] = 0;
} else {
// 父亲的失败节点存在公共后缀,则将公共后缀的节点作为 curr 的失败节点
fail[currIndex] = nodes.get(temp).children[i];
}
q.addLast(currIndex);
}
}
// 最后让根节点失配时,下一字符依然从根开始尝试匹配,避免查找时特殊逻辑的判断
fail[0] = 0;
}
这份代码是完全按照上面的思路来写的,甚至连变量名的含义都一样,方便对照。
查找
万事俱备,现在我们可以按照字典树与失败指针的路线进行查找了。
从根节点开始,依次匹配。每一节点的成功匹配,均检查是不是某个模式串的结尾,如果是,代表这个模式串匹配成功。然后从根节点开始新一轮匹配(依需求而定)。
如果匹配失败,那么从失败指针指向的节点开始重新尝试匹配这个字符。
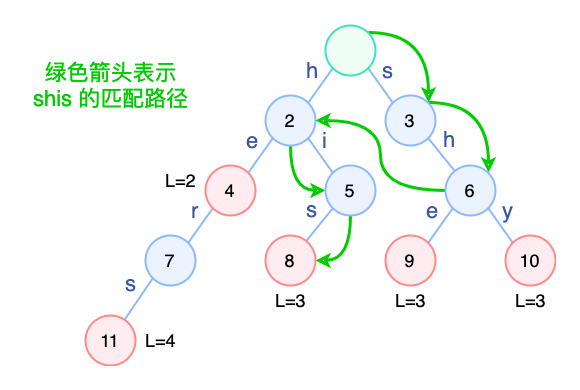
如上图,以搜索字符串 “shis” 为例。在节点 6 失配(因为 6 不包含字符 i),于是跳转到 6 的失败节点 2 再次尝试匹配 i。匹配成功,依次往下最终匹配 his。
void match(@Nullable String str) {
if (str == null) {
return;
}
byte[] bytes = str.getBytes(StandardCharsets.UTF_8);
int pIndex = 0;
int i = 0;
while (i < bytes.length) {
int b = bytes[i] - Byte.MIN_VALUE;
if (nodes.get(pIndex).children[b] != -1) {
// 当前节点包含所需的字符
pIndex = nodes.get(pIndex).children[b];
AcNode p = nodes.get(pIndex);
if (p.pattern != null) {
// 正好是一个模式串的结尾,匹配成功
System.out.println(p.pattern);
// 下一轮从根开始匹配。因为要求每个字符只能被消耗一次(依需求而定)
pIndex = 0;
}
i++;
continue;
}
// 失配
if (pIndex == 0) {
// 只有根节点就失败时,才代表当前字符完全无法匹配,继续下一个字符
// 否则应该从失败指针处再次查找当前字符
i++;
}
pIndex = fail[pIndex];
}
}
优化
某些时候,查找过程中需要连续多次跳转 fail 指针,例如模式集合 { ab, aab, aaab, c },目前的 AC 结构如下:

搜索文本串 “aaac” 时,路径如下:

可以看到,为了搜索潜在的模式串 aaab 我们一直搜索到 6 号节点,然后一步步失败,直到根节点,然后才重新匹配到了 c,要是可以一步到位就好了。
其实跳 fail 的过程很明确:我们要找到存在字符 c 的节点,否则就一直跳。换句话说,无论在哪里失配,最终一定要跳转到字符 x 指向的节点上,这里的 x 指的是导致失配的那个字符。既然这样的话,直接把那个 x 指向的节点作为孩子不就完事了?
还有另一个想法:直接把失败指针指向
x指向的节点。❌ 然后就踩了一个坑。因为一个节点只有1个失败指针。经过优化,具体该指向谁与谁导致了失配有关,也就是说与文本串有关,这个东西是未知的。在我们的例子中,搜索 “aaac”,
6失败时应该跳转到3。但如果搜索 “aaaa”,就得跳转4最后回到6了。所以不能修改失败指针。那为什么作为孩子可以呢?因为一个字符对应一个孩子呀!不同字符不会冲突。
那么 trie 树就变成了 trie 图(有向图)。
具体做法是,在构建失败指针时,对于遍历到的每一个节点:
若它不包含某个字符 x,那么将它失败节点字符 x 所指向的那个节点作为自己的孩子。 这隐含了一个情况:如果失败节点不存在或者同样不包含 x,那么这个位置的指针不会改变。
在我们的例子中,节点 2 不包含字符 c ,它的失败节点的 root 包含 c,指向 3,那么就把 3 作为节点 2 中 c 对应的孩子。
节点 2 不包含字符 d,它的失败节点 root 依然没有 d,令 2[d] = root[d],最终 2[d]=root[d]=-1 没有改变。
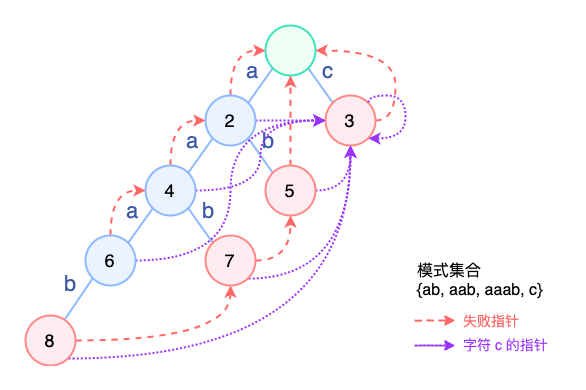
这个图看起来很吓人。冷静一点分析的话,其实挺简单的。
- 对于节点
3,它的失败节点为root,root中c指向3,所以节点3的c原来不存在,现在指向自己。 - 对于节点
4,它失败节点为2,2原来不包含c,但是按照层序遍历的顺序,先前处理的时候,3已经变成了2中c对应的节点了。 因此4中的c也变成了3。 - 其他同理。
如此一来,在节点 6 我们根本不会失配,而是直接跳转到 3,节点 3 恰好是模式串的结尾,模式串长度=1,成功匹配到模式串 c。
特别的,节点 3 的自环看起来很古怪,但不会产生异常。例如文本串 “accd”,从节点 2 跳转到 3,匹配一个 c,然后再次跳转到自己(3 此时拥有字符 c,指向自己),又匹配一个 c,d 失配,不匹配。最终匹配两个 c,符合预期。
尽管理解起来比较困难,代码却非常简单,只需要在构造失败指针的时候添加一行即可:
private final ArrayDeque<Integer> q = new ArrayDeque<>(); // 用于层序遍历的队列
private int[] fail;
void calcFail() {
q.clear();
fail = new int[nodes.size()];
Arrays.fill(fail, -1);
q.addLast(0);
while (!q.isEmpty()) {
int fatherIndex = q.pop();
AcNode father = nodes.get(fatherIndex);
for (int i = 0; i < father.children.length; i++) {
if (father.children[i] == -1) {
// !!!!修改这里!!!!
father.children[i] = nodes.get(Math.max(fail[fatherIndex], 0)).children[i];
continue;
}
int currIndex = father.children[i];
int temp = fail[fatherIndex]; // temp 为当前节点 curr 父节点的失败指针
while (temp != -1 && nodes.get(temp).children[i] == -1) {
// 若父亲的失败节点不为空,但是不存在公共后缀,则继续向上从这个节点的失败节点寻找
temp = fail[temp];
}
if (temp == -1) {
fail[currIndex] = 0;
} else {
// 父亲的失败节点存在公共后缀,则将公共后缀的节点作为 curr 的失败节点
fail[currIndex] = nodes.get(temp).children[i];
}
q.addLast(currIndex);
}
}
// 最后让根节点失配时,下一字符依然从根开始尝试匹配,避免查找时特殊逻辑的判断
fail[0] = 0;
}
⚠️ 这个优化破坏了字典树的结构,使之失去了动态添加模式串的能力。优化前,若模式集合变更,只需要重新计算失败指针即可。现在不得不重新构造字典树,再来计算。