LeetCode42 对撞指针的运用

引例 - 装水容器

还是从一道相对简单的问题入手：LeetCode11 - Container With Most Water

问题概要：

给一个数组，代表一系列墙壁的高度。要求选出两个墙壁，使它们能够储存最多的水。并且：

• 忽略墙壁的厚度
• 忽略选定的墙壁之间的墙壁

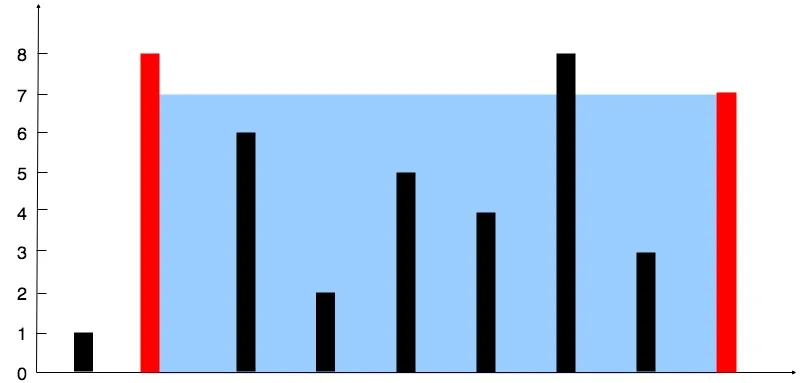
暴力解法

可以轻松想出一个暴力解法：遍历所有墙壁的组合，找出容积最大的一个。

class Solution {
  fun maxArea(height: IntArray): Int {
    var maxArea = 0
    for (a in height.indices) {
      for (b in a + 1 until height.size) {
        maxArea = max(maxArea, min(height[a], height[b]) * (b - a))
      }
    }
    return maxArea
  }
}

这个解法时间复杂度是 O(n²)，空间复杂度是 O(1)

优化

有些题目，比如 LeetCode1 - Two Sum，可以通过缓存一些数据，去除一层循环，优化到 O(n) 级别。但分析一下这一题，循环中不会用到任何之前的数据，即：每一次循环都需要实时数据进行实时计算。因此这个思路不可行 ❌

此时，一个典型的算法出现了——双指针，在这个例子里可以更具体地说是对撞指针。

对撞指针指使用两个指针（下标）初始情况下分别指向数组两端，根据一定规则每次向中间移动一个指针。当两者相遇时算法结束。

针对这一题，不难看出容积 v = min(a,b) * (p2-p1)，其中 a,b 分别是 p1,p2 对应的值。初始状态下，后一个因子已经达到最大。因此若希望指针移动的过程中可以得到更大的结果，则第一个因子必须变大。而第一个因子（min(a,b)）又只受 a,b 较小一方的影响。 假设这样一个情况：

4, 8, 1, 2, 9
p1          p2

此时有两种选择：

1. 把 p1 后移。那么有两种可能的结果：
   1. 新的数 >4，可能得到更大的容积 ✅
   2. 新的数 <=4，只会得到更小的容积 ❌
2. 把 p2 前移。也是两种情况：
   1. 新的数 >4，但只会得到更小的容积 ❌ 因为第一个因数还是取 p1=4 不变，宽度却变小了。
   2. 新的数 <=4，显然，容积更小了 ❌

由此可见，若希望容积变大，唯一的可能性就是移动较小的指针。这就是本题对撞指针中所谓的「按一定规则移动指针」。

a=b 的边界情况无需特殊处理，随便选一个移动就好。此时容积一定会减小，但不能由此认为算法应该终止，因为后面依然有变大的可能。

优化后代码

class Solution {
  fun maxArea(height: IntArray): Int {
    // 只有移动小的一边，结果才有可能变大。
    var maxArea = 0
    var a = 0
    var b = height.size - 1
    while (a < b) {
      maxArea = max(min(height[a], height[b]) * (b - a), maxArea)
      if (height[a] < height[b])
        a++
      else
        b--
    }
    return maxArea
  }
}

此时时间复杂度降到了 O(n) 🍻

正餐 - 收集雨水

LeetCode42 - Trapping Rain Water

问题概要：

给一个数组，代表一系列墙壁的高度。求总共可储存多少雨水。并且：

• 墙壁厚度不可忽略
• 墙壁会占用容积

暴力解法

如图，可储水的区域有可能是不规则的，因此不能如法炮制上一题使用 宽x高 直接计算。一个自然的想法就是：分别计算每一列的容积后求和，因为对于每一列，容积要么是 0，要么是规则矩形的面积，很好计算。

略加观察思考，可以得出每一列容积的计算公式：v = min(maxL,maxR) - height。即分别找出它两边最高的墙，取较矮的一个（这和上一题思路一致），减去当前的墙高（因为墙壁会占用容积）。

那么就可以写出对应的代码：

class Solution {
  fun trap(height: IntArray): Int {
    // 单独计算每列的容积 v = min(maxL,maxR)-h
    var total = 0
    for (i in height.indices) {
      val v = maxBoundary(height, i) - height[i]
      if (v > 0)
        total += v
    }
    return total
  }

  private fun maxBoundary(height: IntArray, pos: Int): Int {
    var maxL = 0
    for (i in 0 until pos) {
      maxL = max(maxL, height[i])
    }
    var maxR = 0
    for (i in pos + 1 until height.size) {
      maxR = max(maxR, height[i])
    }
    return min(maxL, maxR)
  }
}

时间复杂度是 O(n²)

优化

观察本题与上一题的公式，它们都有一个 min 函数。借用上一题的思路，可以得出结论：不一定要遍历找出某列两边最高的墙壁。双指针从两头向中间遍历，我们可以自然地记录「当前」的 maxL 与 maxR，如果把其中一个指针作为要计算容积的列，那么它的 maxL 或 maxR 一定有一个是可以准确确定的。至于另一个，我们并不关心，因为如果我们规定只对较矮的一个指针进行操作，那么那个不确定的值本来就不会影响结果（min 函数只取较小的一个）。

比如起始情况：

0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1
p1                               p2

此时 p1 比较矮，那么我们对 p1 进行操作。它的 maxL=0，maxR 无所谓，v = min(0,maxR) - 0 = 0。然后令 p1 右移。

不妨规定 p1 p2 高度相等时依然对 p1 操作。（规定对 p2 操作不影响最终结果），那么循环到如下情况：

0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1
      p1                         p2

此时 p1=0，p2=1，显然应该对 p1 操作。此时 maxL=1 是确定的，maxR 不确定但肯定 >=1。根据公式可以算出 v= min(1,1)-0 = 1

以此类推就可以算出所有列的容积。

整理一下核心步骤：

1. 对较矮的一边进行操作。
2. 若高度低于同侧的最大高度则计算容积；
3. 否则更新最大高度。
4. 向中间移动指针，

优化后代码

class Solution {
  fun trap(height: IntArray): Int {
    var a = 0
    var b = height.size - 1
    var maxL = 0
    var maxR = 0
    var total = 0
    while (a < b) {
      if (height[a] < height[b]) {
        if (height[a] > maxL) {
          maxL = height[a]
        } else {
          total += maxL - height[a]
        }
        a++
      } else {
        if (height[b] > maxR) {
          maxR = height[b]
        } else {
          total += maxR - height[b]
        }
        b--
      }
    }
    return total
  }
}

时间复杂度为 O(n)