LeetCode452/435/135/714 贪心算法

总结

当我们感觉局部最优可以推出全局最优，一时找不到反例时就可以使用贪心算法。所谓「贪心」就是只在眼下找到最好的方法。贪心算法相对比较抽象，不像滑动窗口那么好识别有套路。局部最优有很多种表现形式：例如先处理一部分元素，再处理其他部分。或者先从一个维度处理全部元素，再从另一个维度处理。不要把「局部」狭义地理解成「一部分元素」。

一般来说贪心算法需要先进行某种形式的排序，因为只有在有序序列中才可能找到局部最优，否则必须得遍历整个数组才能找到最优解。

452 爆破气球的最小箭数

传送门

There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array points where points[i] = [xstart, xend] denotes a balloon whose horizontal diameter stretches between xstart and xend. You do not know the exact y-coordinates of the balloons.

Arrows can be shot up directly vertically (in the positive y-direction) from different points along the x-axis. A balloon with xstart and xend is burst by an arrow shot at x if xstart <= x <= xend. There is no limit to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.

Given the array points, return the minimum number of arrows that must be shot to burst all balloons.

这个题目的意思就是给定一堆气球的 x 轴的跨度，把 x 轴想象成边界，从这里开始向 y 轴正方向射箭，问最少几只箭可以射爆全部气球？

局部最优：一支箭尽量射到更多的气球。全局最优：射爆全部气球消耗最少的箭。

已经知道使用贪心思路通常要排序，不妨按照气球在 x 轴的起点坐标排序，怎么才能一次射中更多的气球呢?

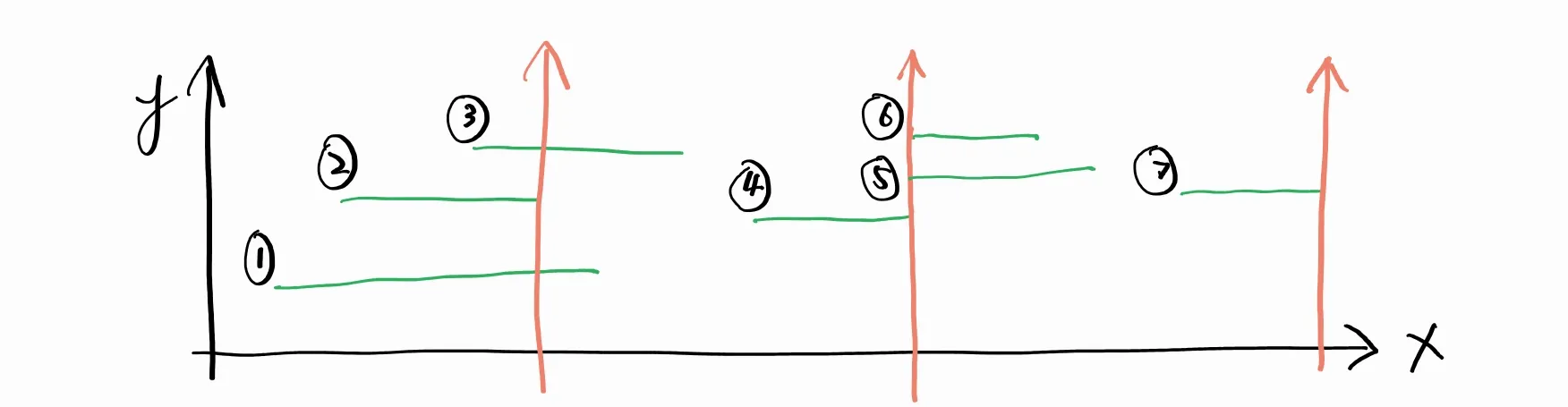
从图中看出，当气球按照起始坐标排序后，只需寻找最小的右边界 R，直到下一个气球的起始位置在 R 之后，就找到了一组最大重叠气球，即：本组所有气球的左边界都小于 R，所有气球的右边界都大于或等于 R 。这组气球需要射箭的位置就是 R。

需要注意的边界条件是：一个气球的结束恰好是另一个气球的开始位置时不视为一组的结束，因为从代码角度，下一个气球可能有相同的起始位置（如图中 5/6 号箭）。直到扫描到 7 的时候才可以断定上一组结束，从而选择在最小结束位置（也就是 4 的右边界射箭）。

代码如下（java）：

class Solution {
  public int findMinArrowShots(int[][] points) {
    if (points.length == 0) return 0;
    Arrays.sort(points, Comparator.comparingInt(o -> o[0]));
    int res = 0;
    int nextBinary = Integer.MAX_VALUE;
    for (int[] point : points) {
      if (point[0] > nextBinary) {
        res++;
        nextBinary = point[1];
        continue;
      }
      nextBinary = Math.min(nextBinary, point[1]);

    }
    return res + 1; // 最后一个气球要射一次
  }
}

435 无重叠区间

传送门

Given an array of intervals intervals where intervals[i] = [starti, endi], return the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping.

这题和上一题射气球有一点类似，都是重叠区间问题。删除最少的区间，等价于保留最多的区间。为了保留尽可能多区间且不重叠。

这里有一个易错点：保留最多的区间不代表优先选择最短的区间，这种局部最优是不能推出全局最优的，比如：

^ Y
|   ---------   ------------
|          ------
-------------------------------> X

如果选择了最短的一个，那么就只能保留这一个区间了，其实最优解是保留那两个长的。

不妨依然按照区间的起始位置排序，只要某区间的起始位置大于上一个区间的结束位置，那肯定就重叠了。此时局部最优为：优先选择右边界小的点，这样才能避免与后边的区间重叠。为啥一定要排序呢？我们不止要考虑右边重叠，还要考虑左边重叠。排序之后相当于是从左向右处理，可以确保正在处理的区间的左边，都是处理过的，专心处理右边就行。

代码（java）：

class Solution {
  public int eraseOverlapIntervals(int[][] intervals) {
    Arrays.sort(intervals, Comparator.comparingInt(o -> o[0]));
    int count = 0;
    int lastRight = Integer.MIN_VALUE;
    for (int[] interval : intervals) {
      if (interval[0] >= lastRight) {
        count++;
        lastRight = interval[1];
      }
      lastRight = Math.min(lastRight, interval[1]);
    }
    return intervals.length - count;
  }
}

135 分发糖果

传送门

There are n children standing in a line. Each child is assigned a rating value given in the integer array ratings.

You are giving candies to these children subjected to the following requirements:

• Each child must have at least one candy.
• Children with a higher rating get more candies than their neighbors.

Return the minimum number of candies you need to have to distribute the candies to the children.

可以看到每个小孩可以得到多少糖果取决于他两边的孩子。这题就是典型的「局部」代表局部角度，而不是局部元素。

按照贪心算法惯例，首先对孩子按照评分从低到高排序。

先只考虑左边，即：任意孩子如果比他左边的评分高，就得到更多的糖果，否则只给 1 粒。然后在考虑右边：任意孩子如果比他右边的评分高，就得到更多的糖果，否则 1 粒。最后得到全局最优：取两趟计算较大的一个。

代码（java）：

class Solution {
  public int candy(int[] ratings) {
    if (ratings.length == 0) return 0;
    int[] candies = new int[ratings.length];
    // 只考虑左边
    candies[0] = 1;
    for (int i = 1; i < candies.length; i++) {
      candies[i] = ratings[i] > ratings[i - 1] ? candies[i - 1] + 1 : 1;
    }
    // 只考虑右边，取大
    for (int i = candies.length - 2; i >= 0; i--) {
      int newValue = ratings[i] > ratings[i + 1] ? candies[i + 1] + 1 : 1;
      candies[i] = Math.max(candies[i], newValue);
    }
    // 计算答案
    int res = 0;
    for (int candy : candies) {
      res += candy;
    }
    return res;
  }
}

714 买卖股票

传送门

You are given an array prices where prices[i] is the price of a given stock on the ith day, and an integer fee representing a transaction fee.

Find the maximum profit you can achieve. You may complete as many transactions as you like, but you need to pay the transaction fee for each transaction.

Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).

这题还有一个简单的版本：买卖股票 II。只要坚持低买高卖就可以获得最高利润，那么局部最优就是：当天获得最高利润。也就是说，如果第二天股票价格涨了，那么今天就买，明天卖。可能有小伙伴好奇，那如果继续涨📈呢？不怕，如果后天涨了，明天卖了之后会再买的，最终结果与今天买明天不操作后天再卖一样。

但这道题给每次卖出加了手续费。所以坚持低买高卖的同时还要减少交易次数。此时局部最优是：在连续获利的最后一天卖出。

其实我们不关心买入/卖出的具体操作，只要计算总获利就行了。所以从代码角度，只要涨幅超过手续费就可以计算利润，这个利润记得扣除手续费。如果连涨注意不要多次扣费（相当于只卖一次）。

代码如下（java）：

class Solution {
  public int maxProfit(in	t[] prices, int fee) {
    int minPrice = prices[0];
    int result = 0;
    for (int i = 1; i < prices.length; i++) {
      if (prices[i] < minPrice)
        minPrice = prices[i]; // 低价买入
      if (prices[i] - minPrice > fee) {
        result += prices[i] - minPrice - fee;
        minPrice = prices[i] - fee; // 下一次如果连涨，就补偿手续费；如果不连涨，minPrice 会自动重置
      }
    }
    return result;
  }
}