LeetCode 动态规划
This page is not available in English yet. (つд⊂)
总结
动态规划通过保存已经计算过的结果,优化计算所有可能性的过程。 下面几种问题都牵扯所有可能性的计算:
优化问题: 在所有可能的解决方案中,寻找用时最短/代价最少的等。 【例】爬楼的最低成本
求所有解: 需要求出所有的情况,而不是选出其中的一个。
【例】斐波那契数列
背包问题: 给定候选物品与限制,求最佳选择方案。
解题步骤
动态规划是一个思想,不是某个具体的算法。它分为好几个步骤,不同步骤要寻找各自的算法。
- 寻找递推公式。 动态规划问题通常包含递归思想,我们要先找到递归的「基本情况」,然后寻找递推公式来得出后续的结果。为此,尝试自顶向下分解问题,思考每一步分解如何倒过来计算下一步的答案。
- 储存子问题的计算结果,避免重复计算。 选择合适的数据结构存储递归中重复计算的东西,通常牵扯到大名鼎鼎的
dp数组。 - 转为迭代。 注意数组右边界情况。
- 优化 dp 数组。 只保留用于下一次迭代的元素。 注意,不是所有问题 dp 数组都可以优化。
优化问题 - 746 爬楼的最低成本
You are given an integer array
costwherecost[i]is the cost ofithstep on a staircase. Once you pay the cost, you can either climb one or two steps.You can either start from the step with index
0, or the step with index1.Return the minimum cost to reach the top of the floor.
按照动态规划的解题步骤:
寻找递推公式
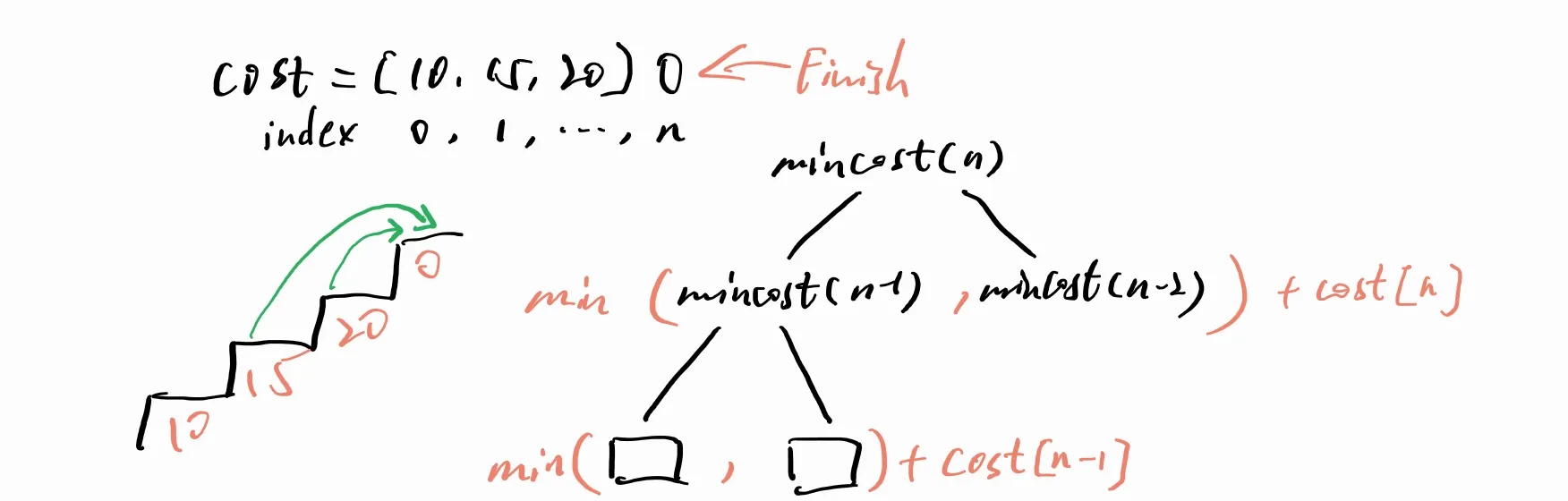 以
以 cost = [10, 15, 20] 为例。要到达楼顶有两个选择:要么从 15 那一级爬,要么从 20 那一级爬。要求最低代价,所以要挑选累计代价最低的一个。而无论是 15 还是 20,到达它们的最低代价都取决于前面的轨迹。这就找到了递归。并且可以得出到达层 n 的最低代价递推公式为:mincost(n) = min(mincost(n-1), mincost(n-2)) + cost[n]。
显然 n=0/1 是我们的基本情况,因为这两级可以作为起始点。
总结一下,得到完整递推公式:
- mincost(i) = min(mincost(i-1), mincost(i-2)) + cost[i]
- mincost(0) = cost[0]
- mincost(1) = cost[1]
可能有小伙伴觉得这题已经解决了,干嘛还要动态规划呢?
这是一个递归算法,递归函数中有两次递归调用,这意味着:
- 时间复杂度为
- 空间复杂度为 (函数栈开销)
显然是不可接受的。
储存中间结果
暴力递归法会产生指数级别的重复运算。比如计算 mincost(i-1) 时必定要计算 mincost(i-2) 与 mincost(i-3),而计算 mincost(i-2) 时还要计算 mincost(i-3),这就重复计算了。可以想象,计算 mincost(i-3) 时往下递归,又会有一大堆重复计算。
这些重复计算的结果就是我们要存储起来的。那么用什么保存?这取决于递归函数的参数。因为我们选择的容器最好可以通过参数来随机访问元素。显然数组是个不错的选择。事实上,大部分题目中都使用数组,就是常见的 dp 数组。这一步的关键是定义清楚 dp 的下标与值代表什么。
这样一样,到达每一级阶梯的最小代价只需要计算一遍,因此时间复杂度降低到 。
到此为止动态规划的核心步骤已经完成了。只是空间复杂度严格来说是 ,因为除了记录中间结果的数组,还有递归的调用栈开销,这里还有优化的空间。
改写迭代
从递推公式我们就能隐约感觉,完全可以从基本情况开始逐步迭代,从而一步步计算最终答案。有了 dp 数组,实现这个目标相对而言轻松许多了。
只需要从前往后遍历我们的 dp 数组,利用同一套递归公式,就可以完成迭代。
唯一要注意的是数组右边界情况。 通常题目要求的答案不在数组中,所以循环完成后应该再手动迭代一次,这才是答案。
虽然空间复杂度没有变化,其实是节省了函数调用栈的开销。
优化 dp 数组
在上面的迭代算法中,不难看出我们一直在使用 dp 数组中最新的两位。既然这样,何不只保留这两位呢?
现在 dp 数组只需要两个元素,每一次迭代先计算新的结果,然后把 dp[1] 挪到 dp[0],把新结果写入 dp[1],就可以继续迭代了。
优化后空间复杂度降低到常量级别 。
代码 (java)
class Solution {
public int minCostClimbingStairs(int[] cost) {
int[] dp = new int[2];
dp[0] = cost[0];
dp[1] = cost[1];
for (int i = 2; i < cost.length; i++) {
int c = cost[i] + Math.min(dp[0], dp[1]);
dp[0] = dp[1];
dp[1] = c;
}
return Math.min(dp[0], dp[1]);
}
}01背包问题
背包问题是动态规划的一类,01 背包又是背包问题的一个子类。
背包问题的典型模型是:给定一些物品,他们各自有不同的重量与价值。有一个固定容量的背包,问最多可以拿取的物品价值是多少。所谓「01 背包」就是每种物品最多只能拿取一次,因此每个物品都有拿/不拿两个状态,由此得名。
实际面试中不太会直接考背包问题,而是让我们自己把原始问题转化为背包模型去解决。现在先不说题目本身,得把背包问题通用的理论搞明白才行。
理论
寻找递推关系
很多背包问题的文章都从 dp 数组讲起,我为了加强对动态规划通用解题步骤的理解,这里依然先寻找递推公式,从递归写法开始。背包问题的递推公式是二维的,一个维度是候选物品,另一个维度是背包容量。我们定义递归函数如下:
/**
* @param weight 物品的重量
* @param value 物品的价值
* @param i 允许拿取 [0,i) 的物品
* @param cap 背包容量
*/
private int maxValue(int[] weight, int[] value, int i, int cap)假设每个物品的价值都大于 0,那么基本情况就是:没有候选元素,或背包容量为 0,那么可拿取的最大物品价值也是 0。
非基本情况下,对于当前物品(下标为 i-1 的物品)有两个选择:拿或不拿。决策树如下:
graph TB A[/是否超过总容量/] A --是--> B[不拿] A --否--> C[/拿了是否增加总价值/] C --否--> B C --是--> D[拿取]
初学的小伙伴可能好奇,拿了不是一定增加总价值吗?
其实不是的,拿了这个物品留给其他物品的容量就少了,但这个物品的价值不一定有其他物品高。
这两种选择的总价值计算方法如下:
- 不拿:把总容量全部分配给 [0, i-1) 的物品去选取。
- 拿:把总容量减去这个物品的重量,然后分配给 [0, i-1) 的物品选取,它们的价值加上这个物品的价值,就是总价值。
这就是递推关系啦。
代码如下:
private int maxValue(int[] weight, int[] value, int i, int cap) {
if (i == 0 || cap == 0) return 0; // 基本情况
// 如果不拿这个(物品,那么所有容量都分配给前面的物品。
int notTake = maxValue(weight, value, i - 1, cap);
if (weight[i - 1] > cap) {
// 这个物品超过了背包的总容量,肯定不能拿
return notTake;
}
// 如果拿这个物品,那么留给前几个物品的容量就是总容量减去这个物品重量
// 此时的总价值是前几个物品的价值加上当前这个物品的价值
int take = maxValue(weight, value, i - 1, cap - weight[i - 1]) + value[i - 1];
return Math.max(notTake, take);
}
// 调用
public int maxValue(int[] weight, int[] value, int cap) {
return maxValue(weight, value, weight.length, cap);
}现在尝试用数组缓存中间结果,省掉重复的计算。我们的递归函数有两个变量 i 和 cap,所以缓存数组是二维的,可以这么定义:
// dp[i][c] 表示从 [0,i) 个物品中挑选,总容量为 c,可拿取的最大价值是多少
int[][] dp = new int[weight.length + 1][cap + 1];注意,根据 dp 的定义,dp[weight.length][cap] 是有意义的,表示从所有物品中挑选,容量就是给定的最大容量,因此建立 dp 数组的时候记得给容量 +1。缓存之后的代码就不放了,比较简单,递归函数的结果存入缓存,递归计算之前先从缓存里检查一下就行。
改写迭代
根据 dp 数组的定义,以及递归写法中的基本情况,可以得出初始化 dp 数组的方法:第一行和第一列全部置 0。
- 第一行置 0:无论容量多大,没有可以拿取的东西,则最大价值为 0.
- 第一列置 0:无论有多少东西可以拿,容量为 0,则最大价值为 0.
(java 中默认是 0,不用设置了)
那么迭代方向呢?同样从递归写法中可以看出,要计算 dp[i][c],需要 dp[i-1][c-?],这里的 ? 可能是大于等于 0 的任何数。换句话说,要计算一个元素,需要它上一行(截止到 c 列)的每一个元素。那么从上往下依次迭代每一行就行了。
代码如下:
public int maxValue(int[] weight, int[] value, int cap) {
// dp[i][c] 表示从 [0,i) 个物品中挑选,总容量为 c,可拿取的最大价值是多少
int[][] dp = new int[weight.length + 1][cap + 1];
for (int row = 1; row <= weight.length; row++) {
for (int curCap = 1; curCap <= cap; curCap++) {
int notTake = dp[row - 1][curCap];
// 别忘了 row 表示可以拿 [0,row) 的物品,所以当前物品是 row-1
if (weight[row - 1] > curCap) {
dp[row][curCap] = notTake;
} else {
int take = dp[row - 1][curCap - weight[row - 1]] + value[row - 1];
dp[row][curCap] = Math.max(take, notTake);
}
}
}
return dp[weight.length][cap];
}优化 dp 数组
这里有个更专业的名字,叫改写滚动数组。
既然对于每一个元素的计算,只需要其上一行的元素,那也就只需保留一行历史记录就行,加上当前计算的一行,一共两行。这一步优化也不难,就不单独给出代码了。
更进一步,其实只要一行数组,也就是一维数组就够了,把新的一行的计算直接覆盖到数组里。不过此时要求从右往左计算。一开始转为迭代时,我们总结要计算一个元素,可能需要它上一行(截止到 c 列)的每一个元素。当时「截止到 c 列」没有起到什么作用,现在就很关键了。
假如从左往右计算,计算完 dp[c],它的数值就被覆盖了。那么计算 dp[c+1] 参考的就是新的 dp[c],倒过来计算就可以解决这个问题。同时,对于「当前物品重量超过了容量」这一情况,直接忽略不更新数组就行。
如果从左往右算,相当于同一个物品可以拿取多次,具体见下面完全背包问题的理论部分。
代码如下:
public int maxValue(int[] weight, int[] value, int cap) {
int[] dp = new int[cap + 1];
for (int row = 1; row <= weight.length; row++) {
for (int curCap = cap; curCap > 0; curCap--) {
if (weight[row - 1] <= curCap) { // 容量足够放下当前物品
int notTake = dp[curCap];
int take = dp[curCap - weight[row - 1]] + value[row - 1];
dp[curCap] = Math.max(take, notTake);
}
}
}
return dp[cap];
}拓展问题
这些问题帮助理解背包 dp 数组的本质,而不只是背代码。
拓展问题 1:未优化 dp 时,能否按行从右往左计算?
可以。只要上一行计算完毕了,当前行怎么算都行。随机算都行。而我们的起始行是手动填充的,视为计算完毕。
拓展问题 2:未优化 dp 时,先迭代计算不同物品,再计算不同容量行不行?也就是列优先计算。
可以。反正计算某元素,只需要它上一行截止到 c 列的元素,所以列优先计算也满足这个条件。
拓展问题 3:优化 dp 后能否列优先计算?
不可以。此时的 dp 只能保存一行数据,所以必须按行计算,才能确保 dp 里的数据是「上一行」的数据。
416 - 分割数组
Given a non-empty array
numscontaining only positive integers, find if the array can be partitioned into two subsets such that the sum of elements in both subsets is equal.简单说,就是看能否把一个数组分割成和相等的两部分。
转化为背包问题
猛一看这题和背包没什么关系。这才是面试题目的常态。
分成两个和相等的数组,那每一个数组的和肯定是原先和的一半。这句话都想不通的请先去睡一觉 💤 或者眺望一下远方。
注意一个小坑:如果原先和是奇数,那必然不可能分成两个和一样的数组。
可以这么建模:
- 背包的容量是原先和的一半。
- 每一个元素就是一个物品,其重量和价值都是元素本身。
- 每个元素只能选取一次。
- 求,能否把背包刚好装满。
瞧,这就是 01 背包问题了。
「刚好装满」和传统背包问题问法不太一样,但实际没啥区别。为了装满,肯定要尽可能地多装,只需要最后判断一下,这个尽力多装的结果,有没有塞满就行。
代码 (java)
class Solution {
public boolean canPartition(int[] nums) {
int sum = Arrays.stream(nums).sum();
if (sum % 2 != 0) return false;
int half = sum / 2;
int[] dp = new int[half + 1];
for (int row = 1; row <= nums.length; row++) {
for (int cap = half; cap > 0; cap--) {
if (cap >= nums[row - 1]) { // 能不能塞下当前元素?
// dp[cap] (更新前): 不要当前元素,能塞多少?
// dp[cap - nums[row - 1]]: 塞了当前元素,剩余空间最多塞多少?
dp[cap] = Math.max(dp[cap], dp[cap - nums[row - 1]] + nums[row - 1]);
}
}
}
return dp[half] == half; // 塞满了吗?
}
}494 - 目标和
You are given an integer array
numsand an integertarget.You want to build an expression out of nums by adding one of the symbols
'+'and'-'before each integer in nums and then concatenate all the integers.
- For example, if
nums = [2, 1], you can add a'+'before2and a'-'before1and concatenate them to build the expression"+2-1".Return the number of different expressions that you can build, which evaluates to
target.
这道题不再是求最值,而更像是组合问题,所以递推关系式也不是 max 函数了,有一点变化。
转为背包问题
这题可以这么理解:尝试把数组分为和分别为 A 与 B 的两部分。A 部分元素全部添加正号,B 部分全部添加负号,则题目所求目标可转化为 A-B=target。显然 A+B=Sum,Sum 就是所有元素的和。综合这两个式子可以得出 A=(target+Sum)/2。
类比 416 那道题,现在可以转为背包问题了:背包容量为 (target+Sum)/2,有多少种选取元素的组合可以装满它?
注意两个细节:
- 如果
target > Sum或target < -Sum,则无论如何也无法达到要求,此时结果为 0。 - 如果
(target+Sum)/2是奇数,也无法达到要求。
现在 dp[c] 定义为:容量为 c 的背包,有多少种选取元素的组合可以装满它。显然 dp[0]=1,因为一个没有容量的背包,只要什么都不选就“满了”。「什么都不选」也是一种选择方案,且「没有候选元素」也符合「什么都不选」的条件。
注意:容量为 0 不代表不能选取任何元素,比如 0 元素就不占用容量。
每遇到一个新的候选元素,还是有两个选择:拿取或不拿。但是这里不是求最大价值,而是可能的方案数,因此拿或不拿都是一种方案,两者的结果应该相加。
- 拿取:新方案数是之前的元素填满剩余容量的方案数。
- 不拿:新方案数是之前的元素填满全部容量的方案数。
可能有同学好奇,这里似乎没有判断「正好装满」。那是因为
dp定义为满足条件的方案数,如果不能正好装满则方案数为 0。同时动态规划有「无后效性」,即当前状态的计算依赖上一个状态,而无需关心上一个状态如何计算出来(以及是否正确)。那么整个算法的正确性依赖初始状态。初始状态是我们自己定义的:dp[0]=1,dp[?]=0 (?>0),可以保证正确。所以代码中不用额外判断了。那为什么 416 题需要判断呢?因为那一题的
dp仅仅代表塞进背包的值,「是否装满」不属于 dp 的一部分,自然也不被算法本身所保证。
代码 (java)
class Solution {
public int findTargetSumWays(int[] nums, int target) {
int sum = Arrays.stream(nums).sum();
if (Math.abs(target) > sum) return 0;
if ((target + sum) % 2 != 0) return 0;
int cap = (target + sum) / 2;
// dp[c] 表示容量为 c,有多少个数字的组合能装满
int[] dp = new int[cap + 1];
dp[0] = 1;
for (int row = 1; row <= nums.length; row++) {
//
for (int c = cap; c > 0; c--) {
if (cap >= nums[row - 1]) {
// dp[c]: 不选取当前数字,只选之前的数字,有多少个组合能装满
// dp[c - nums[row - 1]]: 选取当前数字,再从之前的数字中选一些,有多少个组合能装满
dp[c] = dp[c] + dp[c - nums[row - 1]];
}
}
}
return dp[cap];
}
}完全背包问题
理论
务必先看完前面 01 背包的理论再来看这个。
完全背包与 01 背包唯一的区别是:每个物品都有无限个,即每个物品可以多次放入背包。
在 01 背包中对于每个物品只有两个选择:拿与不拿。而在完全背包中有多个选择:不拿或拿 N 个,我们需要在所有选项中取总价值最大的一个。当然,也不是无限制拿的,需要容量足够才行。也就是说最多可以拿的个数,是把所有容量全部分配给当前物品,所能容纳的个数。
搞清了这个,完全背包问题的递归算法就不难了:
/**
* @param i 允许拿取下标为 [0,i) 的物品
* @param cap 容量限制
* @return 可以拿取的最大物品价值
*/
private int maxValue(int[] weight, int[] value, int i, int cap) {
if (i == 0 || cap == 0) return 0; // 基本情况
int result = 0;
// 分别计算不拿、拿 N 个当前物品的情况,取价值最大的一个
for (int count = 0; count <= cap / weight[i - 1]; count++) {
// 取 count 个当前物品,其价值为 value[i - 1] * count
// 留给其他物品的容量为 cap - weight[i - 1] * count
int newValue = maxValue(weight, value, i - 1, cap - weight[i - 1] * count) + value[i - 1] * count;
result = Math.max(result, newValue);
}
return result;
}
// 调用
public int maxValue(int[] weight, int[] value, int cap) {
return maxValue(weight, value, weight.length, cap);
}可以看到表现在代码中唯一的区别是拿取当前物品的策略。其他的框架是一样的。那我们就快进到优化后的 dp 数组。
public int maxValue(int[] weight, int[] value, int cap) {
// dp[c] 表示容量为 c,最多可以拿取多少价值的物品。
int[] dp = new int[cap + 1];
dp[0] = 0; // 没有可拿的物品且容量为 0,则最大拿取价值为 0
for (int i = 1; i <= weight.length; i++) {
// 允许拿取下标为 [0,i) 的物品
for (int curCap = 0; curCap <= cap; curCap++) {
if (weight[i - 1] <= curCap) {
dp[curCap] = Math.max(dp[curCap], dp[curCap - weight[i - 1]] + value[i - 1]);
}
}
}
return dp[cap];
}在 01 背包中我们强调,优化后的 dp 数组必须从右往左遍历,这里相反,必须从左往右遍历。
开始遍历新的物品 i 时,dp[c] 相等于未优化时的「上一行」,它意思是容量为 c 只允许选取 [0, i-1) 的物品,装满后的最大价值是多少。此时新增允许拿取下标为 i-1 的物品,并更新最大价值。
接着遍历下一个容量 c+1,此时 dp[c] 的含义发生了变化,相等于未优化时的「当前行」,它意思是容量为 c,允许拿取 [0, i) 的商品,装满后的最大价值是多少。但是外层循环 i 没变,相当于有机会再拿一次 i-1 商品。在这个商品大循环中,容量小循环每一次都有机会多拿一个 i-1 商品。由此实现了允许重复拿取同一商品的策略,也是和 01 背包在代码层面的差别。
优化 dp 后能否列优先计算?
那时另一个需求了。行优先计算(外层遍历物品)得出的是组合数。列优先计算(外层遍历容量)得出的是排列数。具体看下面 377 的例子。
518 兑换硬币 II
You are given an integer array
coinsrepresenting coins of different denominations and an integeramountrepresenting a total amount of money.Return the number of combinations that make up that amount. If that amount of money cannot be made up by any combination of the coins, return
0.You may assume that you have an infinite number of each kind of coin.
The answer is guaranteed to fit into a signed 32-bit integer.
这题可以类比 494-目标和,这俩都是组合问题而不是求最值,因此状态转移公式都应该是加法而不是 max 函数。区别在于本题一个硬币允许选取多次,是完全背包问题。
转为完全背包问题
题目的描述可以等价改写成:钱包容量为 amount,coins 是可供选择的硬币,每个硬币可拿取多次。问有多少中组合正好装满钱包。直接套用公式不难做出来,但为了加深理解,这里还是一步步来分析。
dp[c] 数组定义为:容量为 c 的钱包,有多少种硬币组合可以装满它。默认情况下没有任何硬币可供选择,钱包容量为 0,恰好可以满足要求(什么也不拿也是一种方案)因此 dp[0]=1。
遇到一个新的可供选择的硬币 i 时,dp[c] 表示从 [0,i-1) 中选择硬币,容量为 c,有多少中组合装满。此时有两个选择:
- 不选取新的硬币,答案为用
[0,i-1)的硬币装满,有多少个组合。 - 拿取新硬币,答案为用
[0,i-1)的硬币装满剩余的容量,有多少个组合。
两个方案的答案加起来作为新的值更新到 dp[c] 上。接着从左往右遍历到 dp[c+1],此时 dp[c] 已更新,其含义是:从 [0,i) 中选择硬币有多少个方案,现在依然有两个选择:
- 不再次拿取当前硬币。
- 再拿一次当前硬币。
依次类推,循环到 dp[amount] 时就可以得出允许多次拿取某一硬币,总共有多少种方案。
代码 (java)
class Solution {
public int change(int amount, int[] coins) {
// dp[c] 表示容量为 c 时有多少个组合可以正好装满
int[] dp = new int[amount + 1];
dp[0] = 1; // 容量为 c,无可选硬币时,只有一个方案:什么都不选
for (int i = 1; i <= coins.length; i++) {
// 允许选取下标为 [0,i) 的硬币
for (int cap = 0; cap <= amount; cap++) {
if (cap >= coins[i - 1]) {
dp[cap] = dp[cap] + dp[cap - coins[i - 1]];
}
}
}
return dp[amount];
}
}377 - 组成和 IV
Given an array of distinct integers
numsand a target integertarget, return the number of possible combinations that add up totarget.The test cases are generated so that the answer can fit in a 32-bit integer.
Note that different sequences are counted as different combinations.
乍一看和上一题差不多,但本题不同的选取顺序视为不同的方案。
排列问题
在上一题中我们按行遍历,它的核心思想是:对于固定的可选物品范围,随着容量增大,能否尽力多拿几个最新的物品。虽然动态规划解法无法得出选择的方案详情,但我们可以想象出来,这样遍历得出的方案,总是按照物品本身的顺序排列的。
比如 nums=[1,2,3], target=4,算法给出的答案是 4,脑补一下,这 4 个方案其实是这样的:
1. {1, 1, 1, 1}
2. {1, 1, 2} <- 2 在 1 后面
3. {2, 2}
4. {1, 3} <- 3 在 1 后面如果改成按列遍历,其核心思想就变成了:对于固定的容量,随着可选物品范围的增大,能否拿一个最新的物品。到新的一轮容量大循环时,再依次看看能不能基于之前大循环的所有方案再拿一个当前物品,这样对物品的拿取就被分散到了不同的循环中。
比如 target=3, i=1 时,只允许拿 1 这个数字,但这个限制只对当前轮有效。之前大循环 target=0/1/2一共有四个方案:{}, {1}, {1,1}, {2},分别基于这四个方案尝试再拿一个 1,所以除了 {1,1,1} 这个方案外,{2,1} 也可以,当然,{1,2} 是不行的,因为当前轮不允许拿 2。
如此一来得到的就是考虑顺序的组合个数了,也称为排列数。
到底求组合还是求排列,关键在于是否需要考虑把物品装入背包的顺序,如果需要考虑就是排列,否则就是组合。
看一下 139 题,很容易混淆。
代码 (java)
理论比较难懂,代码写起来很简单,把内外层循环对调一下就行了。
class Solution {
public int combinationSum4(int[] nums, int target) {
int[] dp = new int[target + 1];
dp[0] = 1;
for (int cap = 0; cap <= target; cap++) { // 外层遍历容量
for (int i = 1; i <= nums.length; i++) {
if (cap >= nums[i - 1]) {
dp[cap] = dp[cap] + dp[cap - nums[i - 1]];
}
}
}
return dp[target];
}
}139 - 分割单词
Given a string
sand a dictionary of stringswordDict, returntrueifscan be segmented into a space-separated sequence of one or more dictionary words.Note that the same word in the dictionary may be reused multiple times in the segmentation.
转化为背包问题
s 是背包,wordDict 是物品列表。问能否用这些物品恰好装满背包。每个单词可以重复使用,因此是完全背包问题。
注意!这是一个顺序敏感题目。也许有同学和我一开始一样,被题目描述误导,认为这题在问能否用字典中的单词组成某个字符串,既然是组成,那顺序就不重要啦。就题目本身来讲确实不重要,但是我们把它转化为了背包问题,转化的过程中注意等价性。背包问题的本质是从一堆物品中选择一些,装满背包。「装满」是个比较模糊的说法,在前几题中,所谓装满就是数值的和与背包容量一致,这种情况下 A+B 还是 B+A 没啥区别。但这题,装满其实有两个含义:
- 字典中的单词可以拼凑出字符串。
- 必须按顺序选取单词装入背包。
相同的字典,选择不同的顺序装,答案可能不一样,我们必须全部都试试才能得到正确结果。所以要按排列问题来算。
然后 dp 数组定义为 dp[c] 表示 [0,c) 的子串能否用字典表示。则遇到一个新词,有两个选择:
- 不使用它。结果是能否用之前的单词表示这个子串。
- 使用它。结果是能否用之前的单词表示剩下的子串。
这两个方案任意一个成立就视为可以表示。
如果把 dp 定义为 bool 型不太理解,可以先定义为 int,含义是:
[0,c)的子串有多少种方式用字典表示。
代码 (java)
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
// dp[c] 表示 [0,c) 子串能否用字典表示
boolean[] dp = new boolean[s.length() + 1];
dp[0] = true;
for (int c = 0; c < s.length(); c++) { // 排列问题,外层遍历背包
for (String word : wordDict) {
if (c >= word.length()) { // 相当于:背包容量必须能放下当前物品
dp[c] = dp[c] || (s.startsWith(word, c - word.length()) && dp[c - word.length()]);
// 如果目前的物品(单词)足够表示(装满背包)了,那么再添加新候选单词必然也能表示
// 所以没必要继续判断,提高性能。
// 但如果 dp 定义为 int 则不建议跳出,因为新的单词可能有新的表示方式,继续计算才符合 dp 的定义
break;
}
}
}
return dp[s.length()];
}
}