LeetCode222 完全二叉树节点数

题目

传送门

According to Wikipedia, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.

Design an algorithm that runs in less than O(n) time complexity.

这个需求的暴力解法是遍历一遍，时间复杂度 $O(N)$ 尚可接受，但这样就失去了这题的意义。这里实现一个时间复杂度为 $O( \log_2 N)$ 的算法。

计算上部节点数

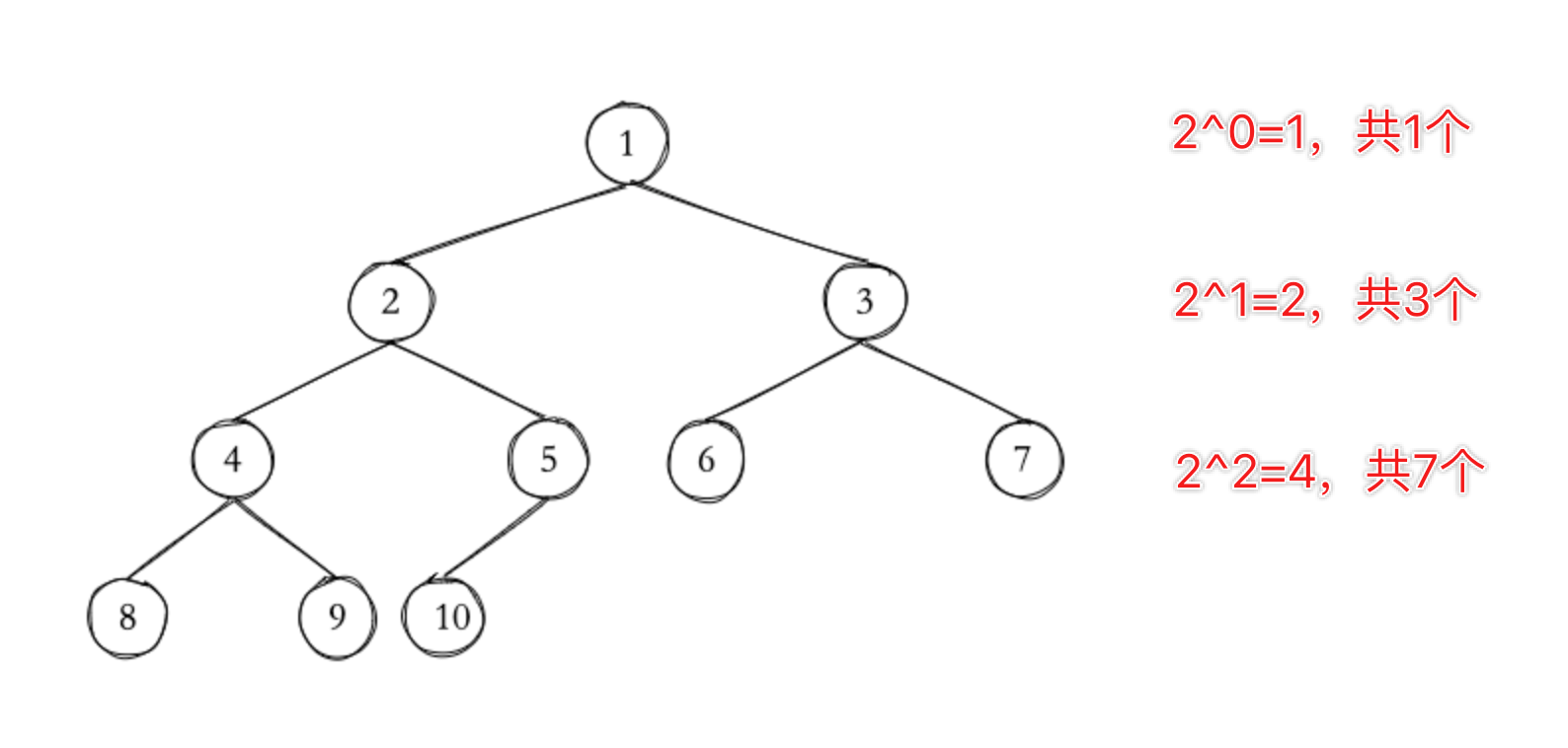
不难得出以下结论：

• 第 h 层的节点数为 $2^{h-1}$ （h 从 1 开始）
• 从根节点到第 h 层总节点数为 $2^h-1$（h 从 1 开始）

那么只要知道了树的高度，就可以立即求出除了最后一层外的节点总数。同时鉴于完全二叉树的特性，只需一直向左子树遍历就可以得到高度。

// 求完全二叉树的高度
private int height(TreeNode root) {
  int res = 0;
  while (root != null) {
    res++;
    root = root.left;
  }
  return res;
}

计算底层节点数

寻找最后一个节点

如图所示，我们给底层节点编号（包括不存在的节点），形式上把它们视为有序数组。也就是说，只需在 $O( \log_2 N)$ 时间复杂度内从这个数组中找到最后一个存在的节点就行。这个需求很轻松地联想到二分查找。

不过需要对二分查找做一点修改：

private int findLastNodeIndex(TreeNode root, int height) {
  // 搜索区间 [l,r]
  int l = 0, r = (int) (Math.pow(2, height - 1) - 1);
  int result = 0;
  while (l <= r) {
    int mid = (l + r) / 2;
    if (nodeExists(root, height, mid)) {
      result = mid;
      l = mid + 1;
    } else {
      r = mid - 1;
    }
  }
  return result;
}

为什么需要额外一个变量 result？ 在本题的场景下，二分查找最终一定会收缩到两个相邻的节点，此时 mid 指向靠左的那个，如果它存在则需要进一步确认它右边的那个是否存在。如果右边的不存在就需要回退到左边，因此需要一个变量存储左边的下标。

通过下标寻找节点

二分查找要求可以通过下标来找到元素，显然二叉树不满足这个要求，还得编写额外的函数来实现。

我们可以把整个二叉树看作是一个标准二分查找的执行过程。现在知道了目标节点的下标，只需把它和当前搜索区间的中点进行对比，再决定往左还是往右查找就行了。

/**
 * 判断最后一行下标为 index 的节点是否存在。index 从 0 开始。
 * @param height 树的高度
 */
private boolean nodeExists(TreeNode root, int height, int index) {
  int l = 0, r = (int) (Math.pow(2, height - 1) - 1);
  for (int i = 0; i < height - 1; i++) {
    // 循环过程中 root 不可能为空
    // 因为完全二叉树除了最后一行，每一行都是满的
    int mid = (l + r) / 2;
    // 这里必须是小于等于
    // mid 与 index 相等时必有 r=l+1, index=l，显然应该向左
    if (index <= mid) {
      root = root.left;
      r = mid - 1;
    } else {
      root = root.right;
      l = mid + 1;
    }
  }
  return root != null;
}

代码（java）

时间复杂度分析：

• 求树高的时间复杂度为 $O(\log N)$
• 最后一层最多有 $2^{h-1}$ 个节点，它几乎是总节点数的一半。同时考虑二分算法，可得出寻找最后一个节点的时间复杂度为 $\log {N/2} = O(\log N)$
• 寻找最后一个节点时，每一次利用下标取节点的时间复杂度均为 $O(h) = O(\log N)$

因此总体时间复杂度为 $O(\log N + \log^2 N)) = O(\log^2 N)$

class Solution {
  public int countNodes(TreeNode root) {
    if (root == null) return 0;
    int height = height(root);
    // 忽略最后一层的节点数
    int count1 = (int) Math.pow(2, height - 1) - 1;
    return count1 + findLastNodeIndex(root, height) + 1;
  }

  private int height(TreeNode root) {
    int res = 0;
    while (root != null) {
      root = root.left;
      res++;
    }
    return res;
  }

  private int findLastNodeIndex(TreeNode root, int height) {
    // 搜索区间 [l,r]
    int l = 0, r = (int) (Math.pow(2, height - 1) - 1);
    int result = 0;
    while (l <= r) {
      int mid = (l + r) / 2;
      if (nodeExists(root, height, mid)) {
        result = mid;
        l = mid + 1;
      } else {
        r = mid - 1;
      }
    }
    return result;
  }

  /**
     * 判断最后一行下标为 index 的节点是否存在。index 从 0 开始。
     * @param height 树的高度
     */
  private boolean nodeExists(TreeNode root, int height, int index) {
    int l = 0, r = (int) (Math.pow(2, height - 1) - 1);
    for (int i = 0; i < height - 1; i++) {
      // 循环过程中 root 不可能为空
      // 因为完全二叉树除了最后一行，每一行都是满的
      int mid = (l + r) / 2;
      // 这里必须是小于等于
      // mid 与 index 相等时必有 r=l+1, index=l，显然应该向左
      if (index <= mid) {
        root = root.left;
        r = mid - 1;
      } else {
        root = root.right;
        l = mid + 1;
      }
    }
    return root != null;
  }
}